Cho \(\Delta ABC\)và M là một điểm nằm trong tam giác.
a) Gọi I là giao điểm của đường thẳng BM và cạnh AC. Chứng minh rằng MA+ MB<IA + IB < CA + CB.
b) Chứng minh rằng MA + MB + MC > nửa chu vi nhưng nhỏ hơn chu vi của \(\Delta ABC.\)
Hướng dẫn: Sử dụng bất đẳng thức tam giác cho các tam giác đinh I và M.
(vẽ hình đầy đủ, giải chi tiết cho mình vs nha)

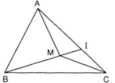
a) Ta lần lượt xét:
\(MA< IA+IM\Leftrightarrow MA+MB< IA+IM+MB\)
\(\Leftrightarrow MA+MB< IA+IB\) (1)
\(IB< CI+CB\Leftrightarrow IA+IB< IA+CI+CB\)
\(\Leftrightarrow IA+IB< CA+CB\) (2)
Từ (1), (2), ta nhận được \(MA+MB< IA+IB< CA+CB,đpcm\)
b) Ta lần lượt xét:
Cộng theo vế (3),(4),(5), ta được:
\(2\left(MA+MB+MC\right)>AB+BC+AC\)
\(\Leftrightarrow MA+MB+MC>\frac{1}{2}\left(AB+BC+AC\right),đpcm.\)
Mặt khác dựa theo kết quả cua câu a), ta có:
\(MA+MB< CA+CB\left(6\right)\)
\(MB+MC< AB+AC\left(7\right)\)
\(MA+MC< BA+BC\left(8\right)\)
Cộng theo vế (6),(7),(8), ta được:
\(2\left(MA+MB+MC\right)< 2\left(AB+BC+AC\right)\)
\(\Leftrightarrow MA+MB+MC< AB+BC+AC,đpcm.\)