Chứng minh n4 + n2 + 1 là hợp số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 11 2017
A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .
CM
10 tháng 5 2017
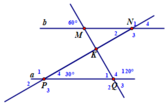
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °
CM
16 tháng 7 2017
a) Phân tích 15 n + 15 n + 2 = 113.2. 15 n .
b) Phân tích n 4 – n 2 = n 2 (n - 1)(n +1).
PT
1
CM
17 tháng 1 2019
Xét các trường hợp chẵn
- n chẵn thì A chia hết cho 2
- n lẽ đặt n = 2k + 1 k ∈ N * .
Ta có
A phân tích được tích của 2 thừa số vậy A là hợp số .
6 tháng 9 2016
Điều kiện: n > 3
Xét 3 số tự nhiên liên tiếp: n^2 - 1; n^2; n^2 + 1, trong 3 số này có 1 số chia hết cho 3
Do n nguyên tố > 3 => n không chia hết cho 3 => n^2 không chia hết cho 3
Mà n^2 - 1 nguyên tố > 3 vì n > 3 => n^2 + 1 chia hết cho 3
Mà n^2 + 1 > 3 => n^2 + 1 là hợp số ( đpcm)
AH
Akai Haruma
Giáo viên
14 tháng 10 2021
Lời giải:
$n^4+3n^3+4n^2+3n+1=(n+1)^2(n^2+n+1)$
Nếu đây là scp thì $n^2+n+1$ cũng phải là scp
Đặt $n^2+n+1=t^2$ với $t$ tự nhiên
$\Leftrightarrow 4n^2+4n+4=(2t)^2$
$\Leftrightarrow (2n+1)^2+3=(2t)^2$
$\Leftrightarrow 3=(2t-2n-1)(2t+2n+1)$
$\Rightarrow 2t+2n+1=3; 2t-2n-1=1$
$\Rightarrow n=0$ (trái giả thiết)
Vậy có nghĩa là $n^2+n+1$ không là scp với mọi $n\in\mathbb{N}^*$
$\Rightarrow n^4+3n^3+4n^2+3n+1$ không là scp với mọi $n\in\mathbb{N}^*$
Ta có đpcm.
CM
3 tháng 1 2020
a) Nếu n = 3k+1 thì n 2 = (3k+1)(3k+1) hay n 2 = 3k(3k+1)+3k+1
Rõ ràng n 2 chia cho 3 dư 1
Nếu n = 3k+2 thì n 2 = (3k+2)(3k+2) hay n 2 = 3k(3k+2)+2(3k+2) = 3k(3k+2)+6k+3+1 nên n 2 chia cho 3 dư 1.
b) p là số nguyên tố lớn hơn 3 nên không chia hết cho 3. Vậy p 2 chia cho 3 dư 1 tức là p 2 = 3 k + 1 do đó p 2 + 2003 = 3 k + 1 + 2003 = 3k+2004 ⋮ 3
Vậy p 2 + 2003 là hợp số
HH
25 tháng 6 2023
a) n không chia hết cho 3 => n chia cho 3 dư 1 hoặc 2
+) n chia cho 3 dư 1 : n = 3k + 1 => n2 = (3k +1).(3k +1) = 9k2 + 6k + 1 = 3.(3k2 + 2k) + 1 => n2 chia cho 3 dư 1
+) n chia cho 3 dư 2 => n = 3k + 2 => n2 = (3k +2).(3k+2) = 9k2 + 12k + 4 = 3.(3k2 + 4k +1) + 1 => n2 chia cho 3 dư 1
Vậy...
b) p là số nguyên tố > 3 => p lẻ => p2 lẻ => p2 + 2003 chẵn => p2 + 2003 là hợp số
1 PHẦN 9
Đề thiếu điều kiện: x thuộc N, x>1
\(n^4+n^2+1=n^4-n+n^2+n+1\)
\(=n.\left(n^3-1\right)+\left(n^2+n+1\right)\)
\(=n.\left(n-1\right).\left(n^2+n+1\right)+\left(n^2+n+1\right)\)
\(=\left(n^2+n+1\right).\left(n^2-n+1\right)\)(1)
Nếu \(\left(n^2+n+1\right).\left(n^2-n+1\right)\) là số nguyên tố => \(\orbr{\begin{cases}n^2+n+1=1\\n^2-n+1=1\end{cases}\Leftrightarrow\orbr{\begin{cases}n.\left(n+1\right)=0\\n.\left(n-1\right)=0\end{cases}}}\)
\(\Leftrightarrow\orbr{\begin{cases}n=0\\n=\pm1\end{cases}\left(KTMĐK\right)}\)
Vậy n4+n2+1 là hợp số