17^2020+11^2020-7^2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.=\dfrac{2019}{2020}\times\left(\dfrac{4}{11}+\dfrac{5}{11}+\dfrac{2}{11}\right)\\ =\dfrac{2019}{2020}\times1=\dfrac{2019}{2020}\\ b.=\dfrac{25}{27}\times\left(\dfrac{17}{14}-\dfrac{1}{14}-\dfrac{2}{14}\right)\\ =\dfrac{25}{27}\times1=\dfrac{25}{27}\)

A = 3+5-7-9+11+13-15-17+19+.....+2011+ 2013-2015-2017+2019+2020
A=(3 +5-7-9)+(11+13-15-17)+....+(2011+2013-2015-2017)+2019+2020
xét dãy số : 3; 11; .....;2011
Dãy số trên có số số hạng : (2011 -3):8+1 = 252
Vậy tổng A là tổng 252 nhóm và 2019 + 2020
Mỗi nhóm có giá trị: 3 + 5 - 7 - 9 = -8
A = -8.252 + 2019 + 2020
A = 2023


ta có \(A=\frac{2020^{10}+2}{2020^{11}+2}=>2020A=\frac{2020^{11}+4040}{2020^{11}+2}=1+\frac{4038}{2020^{11}+2}\)(1)
\(B=\frac{2020^{11}+2}{2020^{12}+2}=>2020B=\frac{2020^{12}+4040}{2020^{12}+2}=1+\frac{4038}{2012^{12}+2}\)(2)
từ 1 and 2 => 2020B<2020A
=> A>B
Ta có B=\(\frac{2020^{11}+2}{2020^{12}+2}\)
suy ra \(B< \frac{\left(2020^{11}+2\right)+2018}{\left(2020^{12}+2\right)+2018}=\frac{2020^{11}+2020}{2020^{12}+2020}=\frac{2020\left(2020^{10}+2\right)}{2020\left(2020^{11}+2\right)}=\frac{2020^{10}+2}{2020^{11}+2}\)
nên A > B

a. 1000 - 121 -79.
= 800.
b. ( - 400 ) - (13 - 47 ).
= - 400 - 13 + 47.
= - 366.
c. ( - 215 ) + 63 + 37.
= - 215 + 100.
= - 115.
d. ( - 147 ) - ( 13 - 47 ).
= - 147 - 13 + 47.
= - 113.
e. 1945 + {( - 1945 ) - 17)}.
= 1945 - 1945 - 17.
= - 17.
f. ( - 2020 ) - {( - 2020 ) - 11 }.
= - 2020 + 2020 + 11.
= 11.
g. ( - 44 ) + {( -14 ) - 30}.
= - 44 - 14 - 30.
= - 88.
h. ( 45 - 3756 ) + 3756.
= 45 - 3756 + 3756.
= 45.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
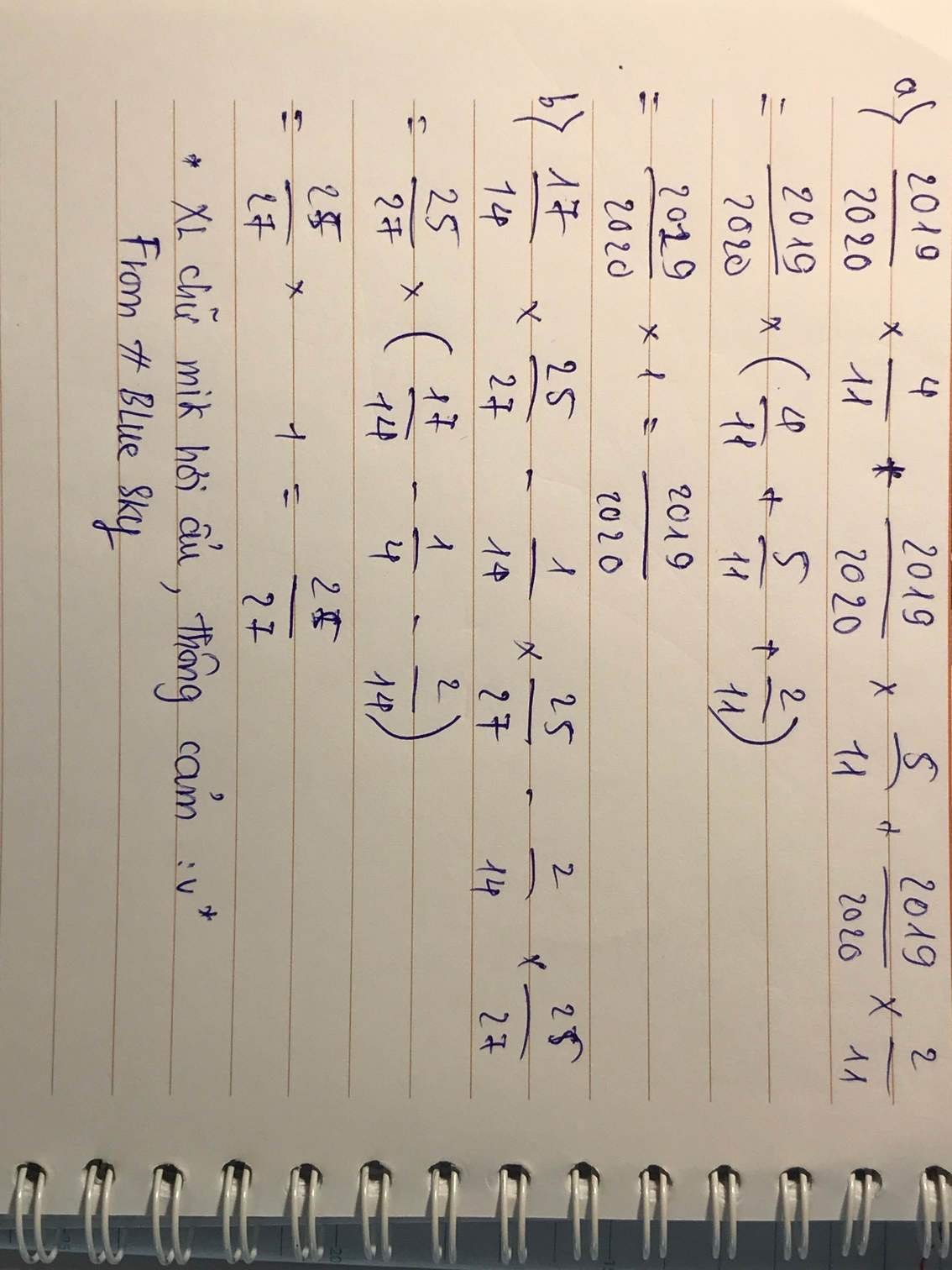
đề bn ơi