Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lấy điểm M thuộc tia AM sao cho M là trung điểm của AM.
Ta chứng minh được:
\(\Delta AMB=\Delta M'MC\left(c.g.c\right)\) suy ra AB = BM'.
\(\Delta AMC=\Delta M'MB\left(c.g.c\right)\Rightarrow AC=BM'\), \(\widehat{CAM}=\widehat{BM'M}\).
Theo định lý tổng ba góc trong tam giác:
\(\widehat{M'AB}+\widehat{BM'A}+\widehat{ABM'}=180^o\Leftrightarrow\widehat{BAM'}+\widehat{ABM'}+\widehat{M'AC}=180^o\).
Mà \(\widehat{DAE}+\widehat{BAM}+\widehat{MAC}=180^o\).
Suy ra \(\widehat{DAE}=\widehat{ABM'}\).
Xét tam giác DAE và tam giác ABM' cóL
DA = AB.
BM' = AC = AE.
\(\widehat{DAE}=\widehat{ABM'}\).
Suy ra \(\Delta DAE=\Delta AB'M\left(c.g.c\right)\).
Suy ra DM = AM' = 2AM. (đpcm).
Câu hỏi của Phạm Tuấn Kiệt - Toán lớp 7 - Học toán với OnlineMath
GT | ΔABC, \(\widehat{A}< 90^o\)
Ax ⊥ AB, AD = AB
Ay ⊥ AC, AE = AC
KL | a, BE=CD
b, BE ⊥ CD
Giải:
a, Vì Ay ⊥ AB
⇒ A1 = 90o <1>
Ax ⊥ AC
⇒ A2 = 90o <2>
Từ <1>,<2> ⇒ A1=A2
Mà \(\widehat{DAC}\) = \(\widehat{A_1}+ \widehat{A_3}\);
\(\widehat{EAC} = \widehat{A_2} + \widehat{A_3}\).
⇒ \(\widehat{DAC}\) = \(\widehat{EAC}\)
Xét ΔDAC và ΔEAB có:
AD = AB (gt)
A1= A2= \(90^o\)
AE =AC (gt)
⇒ ΔDAC = ΔEAB(c.g.c)
b, Vì ΔDAC = ΔEAB(CMT)
⇒ BE⊥ CD( 2 cạnh tương ứng)
Chức bạn học tốt nha! 
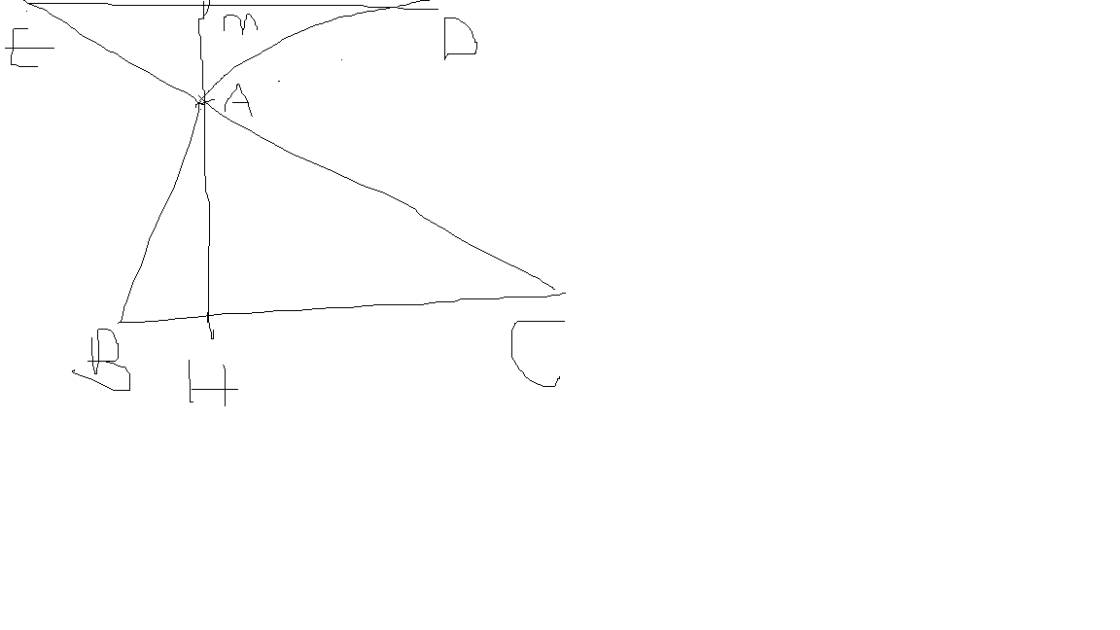
a) Xét ∆AEB và ∆ADC ta có :
EA = AC
DA = AB
EAB = DAC( 2 góc đối đỉnh)
=> ∆AEB = ∆ADC (c.g.c)(dpcm)
=> BE = DC ( 2 cạnh tương ứng) (dpcm)
a)
có \(\widehat{DAC}=90^0+\widehat{BAC}\) ; \(\widehat{BAE}=90^0+\widehat{BAC}\)
\(\Rightarrow\widehat{DAC}=\widehat{BAE}\)
Xét \(\Delta ADC\)và \(\Delta ABE\)
có \(\widehat{DAC}=\widehat{BAE}\)
\(AB=AD\)
\(AC=AE\)
nên \(\Delta ADC=\text{}\Delta ABE\left(c-g-c\right)\)
b)
có\(\Delta ADC=\text{}\Delta ABE\)
nên \(CD=BE\)