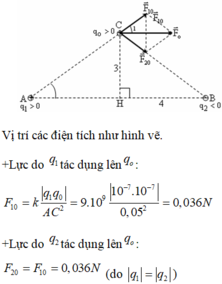
Trong chân không cho 2 điện tích q1=q2=10--7C đặt tại 2 điệm A và B cách nhau 10cm. Tại điểm C nằm trên đường trung trực AB và cách AB 5cm người ta đặt điện tích q0= 10--7C xác định lực điện tổng hợp tác dụng lên q0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2021
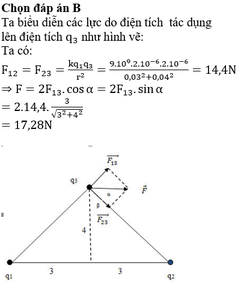
a, Lực điện tương tác giữa hai điện tích là
Fđ = \(9.10^9.\dfrac{\left|-10^{-7}.5.10^{-8}\right|}{0.05^2}=0.018\left(N\right)\)
b, Ta có AC2 + BC2 = AB2 (32 + 42 = 52) nên theo định lí đảo của định lí Pitago ta có tam giác vuông ABC tại C
Lực điện tổng hợp bằng 1 nửa lực điện ở câu A (vẽ hình là thấy)
độ lớn bằng 0.009 N
c, Mình chưa học, nhưng chắc chỉ cần dùng ct là xong
VT
29 tháng 8 2018
Ta có AM = BM = A H 2 + H M 2 = 9 2 + 12 2 = 15 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
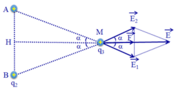
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .6.10 − 6 0 , 15 2 = 24 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ, có độ lớn:
E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 . H M A M = 2 . 24 . 10 5 . 12 15 = 38 , 4 . 10 5 (V/m).
F → = q 3 . E → ; vì q 3 > 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 . E = 5 . 10 - 8 . 38 , 4 . 10 5 = 0 , 192 ( N )
VT
11 tháng 5 2017
Ta có AM = BM = A H 2 + H M 2 = 12 2 + 16 2 = 20 (cm)
Các điện tích q 1 v à q 2 gây ra tại M các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ.
Có độ lớn: E 1 = E 2 = k | q 1 | A M 2 = 9.10 9 .9.10 − 6 0 , 2 2 = 20 , 25 . 10 5 (V/m).
Cường độ điện trường tổng hợp tại M là: E → = E 1 → + E 2 → .
Có phương chiều như hình vẽ.
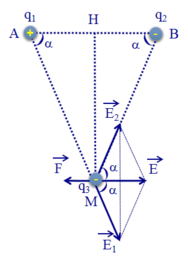
Có độ lớn: E = E 1 cos α + E 2 cos α = 2 E 1 cos α
= 2 E 1 A H A M = 2 . 20 , 25 . 10 5 12 20 = 24 , 3 . 10 5 (V/m).
F → = q 3 E → ; vì q 3 < 0 nên F → cùng phương ngược chiều với E → và có độ lớn:
F = q 3 E = 5 . 10 - 8 . 24 , 3 . 10 5 = 0 , 1215 (N).
Q
4 tháng 8 2021
a, ta thấy CA+CB=AB
\(F_1+F_2=F=k.\left(\dfrac{\left|q_1q_3\right|}{CA^2}+\dfrac{\left|q_2q_3\right|}{CB^2}\right)=14,4+3,6=18\left(N\right)\)
b, CA+AB=CB
\(F=F_1-F_2=k.\left(\dfrac{\left|q_1q_3\right|}{CA^2}-\dfrac{\left|q_2q_3\right|}{CB^2}\right)=3,6-0,567=...\left(N\right)\)
