Cho tập A có n phần tử (n ∈ N*) biết số tập con 3 phần tử nhiều hơn số tập con 2 phần tử 14 tập hợp. Hỏi A có bao nhiêu phần tử?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 10 2018
Đáp án D
Số tập con của A có 8 phần tử C n 8
và số tập của A có 4 phần tử là C n 4
⇒ 26 = C n 8 C n 4 = ( n - 7 ) ( n - 5 ) ( n - 4 ) 1680
⇔ n = 20
Số tập con gồm k phần tử là C 20 k
Khi xảy ra C 20 k > C 20 k + 1
Vậy với k = 10 thì C 20 k đạt giá trị nhỏ nhất.
CM
25 tháng 10 2017
Đáp án D
Ta có:
C n 8 = 26 C n 4 ⇔ n ! 8 ! n − 8 ! = 26 n ! 4 ! n − 4 ⇔ n − 7 n − 6 n − 5 n − 4 = 13 .14.15.16 ⇔ n − 7 = 13 ⇔ n = 20
Số tập con gồm k phần tử của A là: C 20 k ⇒ k = 10 thì C 20 k nhỏ nhất.
CM
7 tháng 8 2018
Đáp án D
Số tập con của A có 8 phần tử C n 8 và số tập của A có 4 phần tử là C n 4
⇒ 26 = C n 8 C n 4 = 4 ! n − 4 ! 8 ! n − 8 ! = n − 7 n − 5 n − 4 1680 ⇔ n = 20.
Số tập con gồm k phần tử là C 20 k .
Khi xảy ra
C 20 k > C 20 k + 1 ⇔ 20 ! k ! 20 − k ! > 20 ! k + 1 ! 19 − k ! ⇔ k + 1 > 20 − k ⇔ k > 9 , 5
Vậy với thì đạt giá trị nhỏ nhất
CM
27 tháng 12 2017
Chọn C
Lời giải. Số tập con có 7 phần tử của tập A là C n 7
số tập con có 3 phần tử của tập A là C n 3
Theo giả thiết, ta có
C n 7 = 2 C n 3 → n = 11
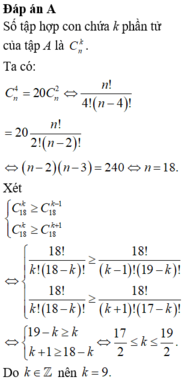
Tập A có n phần tử:
Số tập con có 3 phân tử là: \(C_n^3=\frac{n!}{3!\left(n-3\right)!}=\frac{n\left(n-1\right)\left(n-2\right)}{6}\)
Số tập con 2 phần tử là : \(C_n^2=\frac{n!}{2!\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}\)
Theo bài ra ta có: \(\frac{n\left(n-1\right)\left(n-2\right)}{6}-\frac{n\left(n-1\right)}{2}=14\)<=> \(n^3-6n^2+5n-84=0\Leftrightarrow n=7\)
Vậy tập A có 7 phần tử
mk k hiu cong thức cho lắm