Tìm x, biết:
|x(x−4)|=x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2017
1.
| x + 2 | = | 2 - 3x |
xét 2 trường hợp :
+) TH1 :
2 - 3x = x + 2
-3x + x = 2 + 2
2x = 4
x = 4 : 2 = 2
+) TH2 :
2 - 3x = - ( x + 2 )
2 - 3x = -x - 2
-3x - x = 2 - 2
-4x = 0
x = 0 : ( -4 )
x = 0
bài còn lại tương tự
CM
22 tháng 3 2018
Vì vế trái |x(x − 4)| ≥ 0 với mọi x nên vế phải x ≥ 0.
Ta có: x|x − 4| = x (vì x ≥ 0).
Nếu x = 0 thì 0|0 − 4| = 0 (đúng)
Nếu x ≠ 0 từ x. | x - 4| = x suy ra:
|x − 4| = 1 (chia cả hai vế cho)
⇔ x – 4 = 1 hoặc x – 4 = -1
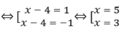
Vậy x = 0, x = 5, x = 3.
18 tháng 8 2021
Bài 1:
Ta có: \(4-2\left(x+1\right)=2\)
\(\Leftrightarrow2\left(x+1\right)=2\)
\(\Leftrightarrow x+1=1\)
hay x=0
Bài 2:
Ta có: \(\left|2x-3\right|-1=2\)
\(\Leftrightarrow\left|2x-3\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
21 tháng 10 2021
\(x^2\left(x^2+4\right)-x^2-4=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
LN
21 tháng 10 2021
x2.(x2 + 4) - x2 - 4=0
⇒ x2.(x2 + 4) - (x2 + 4) =0
⇒ (x2 + 4) .(x2 - 1) = 0
\(\Rightarrow\left[{}\begin{matrix}x^2+4=0\\x^2-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x^2=-4\\x^2=1\end{matrix}\right.\)(loại do x2 ≥ 0) \(\Rightarrow x=\pm1\)
CM
15 tháng 11 2019
Với |x + 1| ≥ 0, |x + 4| ≥ 0 với mọi x nên |x + 1| + |x + 4|
Suy ra: 3x ≥ 0 hay x ≥ 0.
Với x ≥ 0 ta có: x+ 1 > 0 và x + 4 > 0 nên |x + 1| = x + 1 và |x + 4| = x + 4
Ta có: x + 1 + x + 4 = 3x
2x + 5 = 3x
5 = 3x – 2x
5 = x hay x= 5
Vậy x = 5.
CM
26 tháng 9 2019
* Xét x < 1 thì x - 1 < 0 và x – 4 < 0 nên:
|x - 1| = 1 - x; |x - 4| = 4 - x
Ta có: 1 - x + 4 - x = 3x
1 + 4 = 3x + x+ x
5 = 5x
5x = 5
x = 1 (không thỏa mãn điều kiện x< 1).
* Xét 1 ≤ x < 4 thì x – 1 ≥ 0 và x – 4 < 0 nên:
|x - 1| = x - 1; |x - 4| = 4 - x
Ta có: x – 1 + 4 – x = 3x
3 = 3x
3x = 3
x = 3: 3
x = 1( thỏa mãn điều kiện)
* Nếu x ≥ 4 thì x – 1 > 0 và x – 4 ≥ 0 nên:
|x - 1| = x - 1; |x - 4| = x - 4
Ta có: x - 1 + x - 4 = 3x
2x – 5 = 3x
- 5 = 3x – 2x
- 5 = x
x = - 5 ( không thỏa mãn điều kiện)
Vậy x = 1
4 tháng 9 2016
Từ đề bài, ta có các trường hợp sau:
TH1: Cả 3 thừa số đều dương:
Khi đó biểu thức trở thành:
\(\left(x-2\right)+\left(x-3\right)+\left(x-4\right)=2\)
\(\Rightarrow\left(x+x+x\right)-\left(2+3+4\right)=2\)
\(\Rightarrow3x-9=2\)
\(\Rightarrow3x=11\)
\(\Rightarrow x=\frac{11}{3}\)
Do \(\frac{11}{3}-4=-\frac{1}{3}< 0\) ( mâu thuẫn với điều kiện các thừa số đều dương ) nên ta loại.
Vì vế trái \(|x\left(x-4\right)|\ge0\forall x\)nên vế phải \(x\ge0\)
Ta có :\(x|x-4|=x\left(x\ge0\right)\)
Nếu x = 0 thì \(0|0-4|=0\)( đúng)
Nếu \(x\ne0\)thì ta có:
\(|x-4|=1\Leftrightarrow x-4=\pm1\Leftrightarrow\orbr{\begin{cases}x=5\\x=3\end{cases}\left(TM\right)}\)
Vậy x = 0, x = 5, x = 3
|x(x - 4)| = x
<=> |x2 - 4x| = x
Xét 2 trường hợp:
TH1: x2 - 4x = x
<=> x2 - 4x - x = 0
<=> x2 - 5x = 0
<=> x(x - 5) = 0
<=> x = 0 hoặc x - 5 = 0
x = 0 + 5
x = 5
=> x = 0 hoặc x = 5
TH2: x2 - 4x = -x
<=> x2 - 4x - (-x) = 0
<=> x2 - 3x = 0
<=> x(x - 3) = 0
<=> x = 0 hoặc x - 3 = 0
x = 0 + 3
x = 3
=> x = 0 hoặc x = 3
Vậy: x = 0 hoặc x = 5 hoặc x = 3