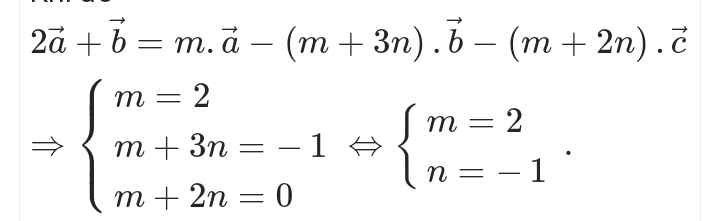giải giùm mình với ạ
giải giùm mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi \(\overrightarrow{v}=\left(a;b\right)\)
d nhận \(\left(4;3\right)\) là 1 vtcp, mà \(\overrightarrow{v}\) vuông góc d \(\overrightarrow{v}=\left(3k;-4k\right)\)
Chọn \(M\left(-1;0\right)\in d\) , do \(T_{\overrightarrow{v}}\left(d\right)=d_1\Rightarrow\) ảnh \(M_1\left(x_1;y_1\right)\) của \(M\) qua phép tịnh tiến \(\overrightarrow{v}\) nằm trên \(d_1\)
\(\left\{{}\begin{matrix}x_1=-1+3k\\y_1=0-4k=-4k\end{matrix}\right.\) \(\Rightarrow M_1\left(-1+3k;-4k\right)\)
Thế vào pt \(d_1\)
\(3\left(-1+3k\right)-4.\left(-4k\right)-2=0\) \(\Rightarrow k=\dfrac{1}{5}\)
\(\Rightarrow\overrightarrow{v}=\left(\dfrac{3}{5};-\dfrac{4}{5}\right)\)

b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot CH=AH^2=AM^2\)

#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n,ln,dem;
int main()
{
cin>>n;
ln=LLONG_MIN;
for (i=1; i<=n; i++)
{
cin>>a[i];
ln=max(ln,a[i]);
}
dem=0;
for (i=1; i<=n; i++)
if (a[i]==max) dem++;
cout<<dem;
return 0;
}


"Trổ tay nghề" lại đi bạn, chụp vầy ai nhìn được chắc mắt gắn chức năng làm rõ hình ảnh :D


Đồng nhất hệ số 2 vế thôi, hệ số các vecto bên vế trái bằng với vế phải (bên vế trái ko có \(\overrightarrow{c}\) nên coi như hệ số của nó bằng 0, do đó \(-\left(2m+n\right)=0\Rightarrow2m+n=0\))

3)\(sin6x.sin2x=sin5x.sinx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x-cos8x\right)=\dfrac{1}{2}\left(cos4x-cos6x\right)\)
\(\Leftrightarrow cos8x=cos6x\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=6x+k2\pi\\8x=-6x+k2\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{7}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
13)\(cosx.cos3x-sin2x.sin6x-sin4x.sin6x=0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(cos2x+cos4x\right)-\dfrac{1}{2}\left(cos4x-cos8x\right)-\dfrac{1}{2}\left(cos2x-cos10x\right)=0\)
\(\Leftrightarrow cos8x+cos10x=0\)
\(\Leftrightarrow2.cos9x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos9x=0\\cosx=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{k\pi}{9}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...
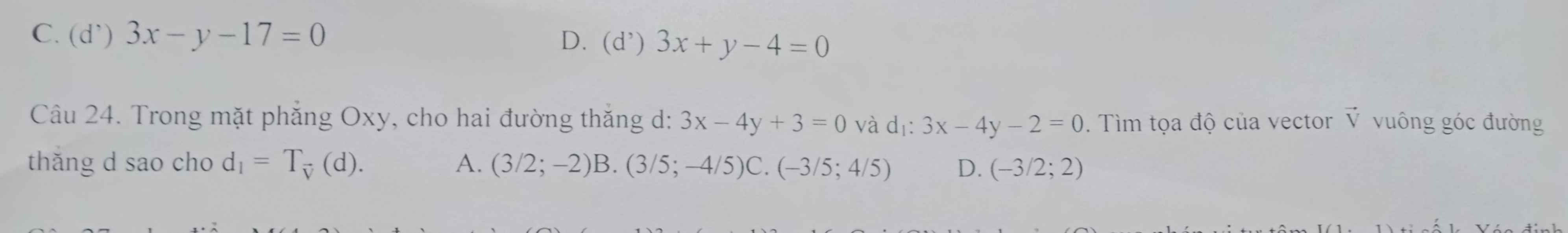


 giải giùm mình với ạ
giải giùm mình với ạ