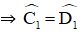Cho 5 điểm A,B,C,D,E chứng minh a/ AB - CD + EA = DB + EC b/ AB + CD + EA = ED - BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chắc là toàn vecto???
a/ \(=\left(\overrightarrow{EA}+\overrightarrow{AB}\right)+\left(\overrightarrow{BC}+\overrightarrow{CD}\right)=\overrightarrow{EB}+\overrightarrow{BD}=\overrightarrow{ED}\)
b/ \(=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CD}+\left(\overrightarrow{DF}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AE}\)

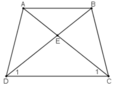
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
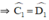
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

ta có : góc CAB=1/2 sđ cung CB
góc CDB = 1/2 sđ cung CB
-> góc CAB= góc CDB
ta lại có : góc ACD =1/2 sđ cung AD
góc ABD =1/2 sđ cung AD
-> góc ACD = góc ABD
xét tam giác EAC và EDB có;
góc EAC=góc EDB( CMT)
góc ACE= góc DBE(cmt)
-> 2 tam giác đồng dạng theo trường hợp g.g
-> EA/EC=ED/EB
-> EA.EB=EC.ED

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.