Một bánh xe bán kính 60 cm quay đều 100 vòng trong thời gian 2 s. Tìm: 1. Tần số và chu kỳ quay. 2. Vận tốc góc và vận tốc dài của một điểm trên vành bánh xe. 3. Gia tốc hướng tâm của một điểm trên nằm trên vành bánh xe.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CT
27 tháng 10 2021
Ta có:
+ Chu kì quay của bánh xe:
+ Tần số:
+ Tốc độ góc:
+ Tốc độ dài của một điểm trên vành bánh xe:
VT
9 tháng 6 2018
Chọn A
ω = 100 2 vòng/s = 50.2π rad/s
= 100π rad/s
Bán kính quỹ đạo của một điểm trên vành bánh xe
R = 60 cm = 0,6 m.
α h t = ω 2 R = 100 . 3 , 14 2 . 0 , 6
= 59157,6 m/s2.
VT
5 tháng 6 2018
Chọn A.
ω = 100 2 vòng/s = 50.2π rad/s = 100π rad/s;
Bán kính quỹ đạo của một điểm trên vành bánh xe : R = 60 cm = 0,6 m.
23 tháng 12 2015
Tần số: \(f=\dfrac{100}{2}=50Hz\)
Vận tốc góc: \(\omega=2\pi f=2\pi .50 = 100\pi (rad/s)\)
Vận tốc dài: \(v=\omega .R = 100\pi . 60 = 6000\pi (cm/s)=60\pi (m/s)\)
VT
11 tháng 6 2018
Bánh xe quay đều với tốc độ góc ω = 2π (rad/s).
Do đó một điểm M thuộc vành ngoài bánh xe cũng quay đều với cùng tốc độ góc ω = 2π (rad/s).
Chu kỳ quay của M: T = 2π/ω = 1 (s).
Tần số quay của M: f = 1/T = 1 Hz.
Tốc độ dài của M: v = R.ω = 0,3.2π = 0,6π (m/s) ≈ 1,9 (m/s).
Gia tốc hướng tâm của M: an = R.ω2 = 0,3.(2π)2 = 12 m/s2.
4 tháng 1 2022
\(v=18km/h=5m/s\)
\(R=25cm=0,25m\)
\(t=1\text{phút}=60s\)
Vận tốc góc của bánh xe là: \(\omega=\frac{v}{R}=\frac{5}{0,25}=20rad/s\)
Tần số quay bánh xe là: \(f=\frac{\omega}{2\pi}=\frac{20}{2\pi}=3,183Hz\)
Số vòng bánh xe quay được trong 1 phút là: \(n=ft=3,183.60=190,98\) vòng
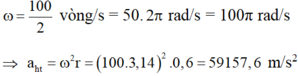
1.Bánh xe quay đều 100 vòng trong thời gian 2s\(\Rightarrow\) \(f=\dfrac{2}{100}=0,02\)vòng/s
Tần số quay của bánh xe: \(f=50\) vòng/s
Chu kì quay: \(T=\dfrac{1}{f}=\dfrac{1}{50}s\)
2.Vận tốc góc của 1 điểm trên vành bánh xe: \(\omega=\dfrac{2\pi}{T}=100\pi\) rad/s
Vận tốc dài của 1 điểm trên vành bánh xe: \(v=\omega.r=100\pi.0,6=60\pi\) m/s
3. Gia tốc hướng tâm của 1 điểm trên vành bánh xe:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(60\pi\right)^2}{0,6}\approx59217,63\) m/s2