Cho các số thực dương x, y ≠ 1 và thoả mãn logxy=logyx, logx(x-y)=logy(x+y). Giá trị của x2+xy+y2bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1+x+y=\sqrt{x}+\sqrt{xy}+\sqrt{y}\)
\(\Leftrightarrow2\left(1+x+y\right)=2\left(\sqrt{x}+\sqrt{xy}+\sqrt{y}\right)\)
\(\Leftrightarrow2+2x+2y=2\sqrt{x}+2\sqrt{xy}+2\sqrt{y}\)
\(\Leftrightarrow2x+2y+2-2\sqrt{x}-2\sqrt{xy}-2\sqrt{y}=0\)
\(\Leftrightarrow\left(x-2\sqrt{xy}+y\right)+\left(x-2\sqrt{x}+1\right)+\left(y-2\sqrt{y}+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-\sqrt{y}\right)^2+\left(\sqrt{x}-1\right)^2+\left(\sqrt{y}-1\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x}=\sqrt{y}\\\sqrt{x}=1\\\sqrt{y}=1\end{cases}}\)
\(\Leftrightarrow x=y=1\)
\(\Rightarrow S=x^{2013}+y^{2013}=1+1=2\)

Đáp án B
Ta có:
log x + 2 y = log x + log y ⇔ log 2 x + 2 y = log 2 x y ⇔ 2 x + 2 y = 2 x y * .
Đặt a = x > 0 b = 2 y > 0 , khi đó * ⇔ 2 a + b = a b và P = a 2 1 + b + b 2 1 + a ≥ a + b 2 a + b + 2 .
Lại có a b ≤ a + b 2 4 ⇒ 2 a + b ≤ a + b 2 4 ⇔ a + b ≥ 8.
Đặt t = a + b , do đó P ≥ f t = t 2 t + 2
Xét hàm số f t = t 2 t + 2 trên 8 ; + ∞ , có f ' t = t 2 + 2 t t + 2 2 > 0 ; ∀ t ≥ 8
Suy ra f t là hàm số đồng biến trên 8 ; + ∞ → min 8 ; + ∞ f t = f 8 = 32 5 .
Vậy gía trị nhỏ nhất của biểu thức P là 32 5 .

Đáp án D
Ta có
y = 10 1 1 − log x z = 10 1 1 − log y ⇔ log y = 1 1 − log x log z = 1 1 − log y ⇔ log y = 1 1 − log z log y = 1 1 − log x ⇒ 1 − 1 1 − log z = 1 1 − log x ⇔ log z − 1 log z = 1 1 − log x ⇔ 1 − log x = log z log z − 1 ⇔ log x = − 1 log z − 1 ⇔ x = 10 1 1 − log z
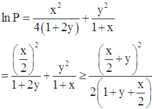
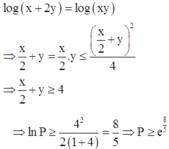
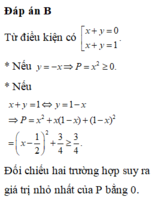
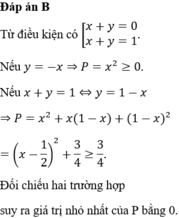
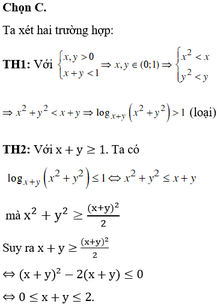
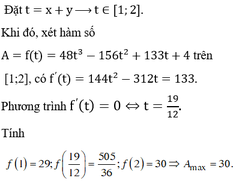

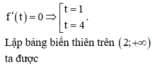
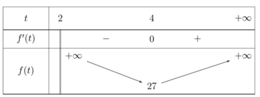

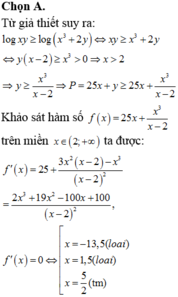
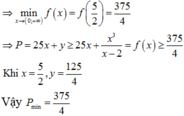
ĐKXĐ: \(x\ne y\)
\(log_xy=\frac{1}{log_xy}\Leftrightarrow log_x^2y=1\Leftrightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=y\left(l\right)\\x=\frac{1}{y}\end{matrix}\right.\)
\(log_x\left(x-\frac{1}{x}\right)=log_{x^{-1}}\left(x+\frac{1}{x}\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+\frac{1}{x}\right)\)
\(\Leftrightarrow log_x\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=1\)
\(\Leftrightarrow x^2-\frac{1}{x^2}=1\Leftrightarrow x^4-x^2-1=0\Rightarrow x^2=\frac{1+\sqrt{5}}{2}\Rightarrow y^2=\frac{1}{x^2}=\frac{-1+\sqrt{5}}{2}\)
\(\Rightarrow x^2+xy+y^2=\frac{1+\sqrt{5}}{2}+1+\frac{-1+\sqrt{5}}{2}=\sqrt{5}+1\)