Tìm điểm cố định của họ đồ thị: y = ax2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, y = ax^2 đi qua B(2;4)
<=> 4a = 4 <=> a = 1
b, bạn tự vẽ
a: Thay x=2 và y=4 vào hàm số, ta được:
\(a\cdot4=4\)
hay a=1
b: Thay x=2 và y=4 vào hàm số, ta được:
4a=4
hay a=1

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 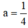
Vậy hàm số: 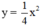
| x | -4 | -2 | 0 | 2 | 4 |
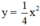 |
4 | 1 | 0 | 1 | 4 |
Đồ thị hàm số:
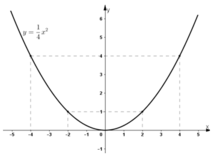

Đồ thị hàm số đi qua A(-2; 1)
⇒
1
=
a
.
(
-
2
)
2
⇒ 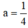
Vậy hàm số: 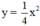
| x | -4 | -2 | 0 | 2 | 4 |
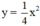 |
4 | 1 | 0 | 1 | 4 |
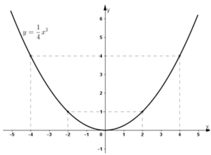
Đồ thị hàm số:

1) Để (P) đi qua điểm A(1;-2) thì
Thay x=1 và y=-2 vào hàm số \(y=ax^2\), ta được:
\(a\cdot1^2=-2\)
hay a=-2


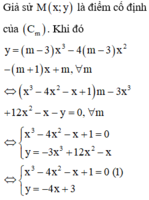
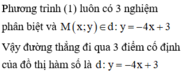

Bạn thay \(x=0\) vào thì \(y=0\) ko phụ thuộc vào a nên đây là điểm cố định
Tốn thời gian hơn thì ta làm như sau:
Giả sử \(A\left(x_0;y_0\right)\) là điểm cố định của hàm số
\(\Rightarrow y_0=ax_0^2\) \(\forall a\)
\(\Leftrightarrow ax_0^2-y_0=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0^2=0\\-y_0=0\end{matrix}\right.\) \(\Rightarrow A\left(0;0\right)\)
Quy tắc tìm điểm cố định thông thường mà bạn?
Dạng \(m.f\left(a;b\right)+g\left(a;b\right)=0\Rightarrow\left\{{}\begin{matrix}f\left(a;b\right)=0\\g\left(a;b\right)=0\end{matrix}\right.\)