xét sự biến thiên và vẽ đồ thị hàm số: y = \(\sqrt[3]{x}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)

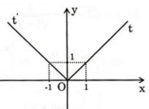
Hàm số y = |x + 1|
Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.
Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1.
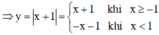
+ Tập xác định: R
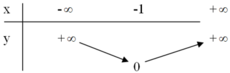
+ Trên (–∞; –1), y = x + 1 đồng biến.
Trên (–1 ; +∞), y = –x – 1 nghịch biến.
Ta có bảng biến thiên :
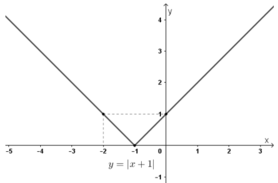
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.
Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.

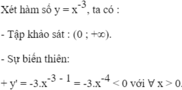
Do đó, hàm số đã cho nghịch biến trên tập xác định.
+ Giới hạn:
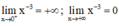
⇒ x = 0 (trục Oy) là tiệm cận đứng của đồ thị hàm số
y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
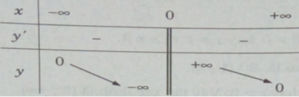
+ Bảng biến thiên:
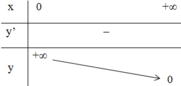
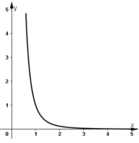
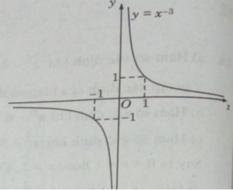
- Đồ thị:

Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
![]()
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
![]()
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.

Hàm số 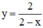
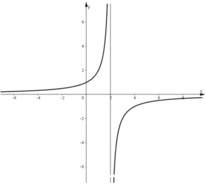
- Tập xác định: D = R\{2}
- Sự biến thiên:
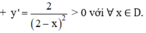
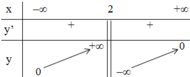
⇒ Hàm số đồng biến trên (-∞; 2) và (2; +∞).
+ Cực trị : Hàm số không có cực trị
+ Tiệm cận: 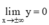
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
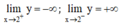
⇒ x = 2 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
- Đồ thị:

Hàm số 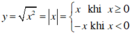 có :
có :
+ Tập xác định D = R.
+ Trên (–∞; 0), hàm số y = –x nghịch biến.
Trên (0 ; +∞), hàm số y = x đồng biến.
Bảng biến thiên :
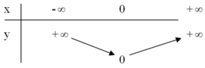
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất: Nửa đường thẳng y = –x giữ lại phần bên trái trục tung.
Phần thứ hai: Nửa đường thẳng y = x giữ lại phần bên phải trục tung.