Question

[Giang Đào]

Câu 1: Cho các hàm số y=f(x), y=g(x), y=\(\frac{f\left(x\right)+2}{g\left(x\right)+1}\)đều có hệ số góc tiếp tuyến tại điểm có hoành độ x=1 giống nhau là k#0. Biết f(1)=a, g(1)=b# -1. Tìm a.

Câu 2: Cho đồ thị (C) y=\(\frac{x+1}{x-2}\)và đường thẳng d: y=x+m. Khi d cắt (C) tại hai điểm phân biệt và tiếp tuyến với (C) Tại hai điểm này song song với nhau thì m bằng bao nhiêu?

Câu 3: Cho hàm số \(y=x^3-3x+2\)

có đồ thị (C). Gọi d là đường thẳng đi qua A(3;20) và có hệ số góc m. Tìm giá trị của m để đường thẳng d cắt (C) tại 3 điểm phân biệt.

Answer 1

[Nguyễn Việt Lâm]

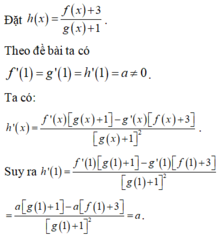
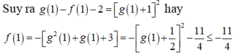
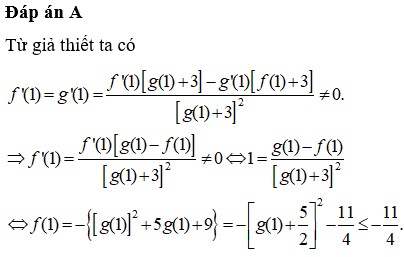
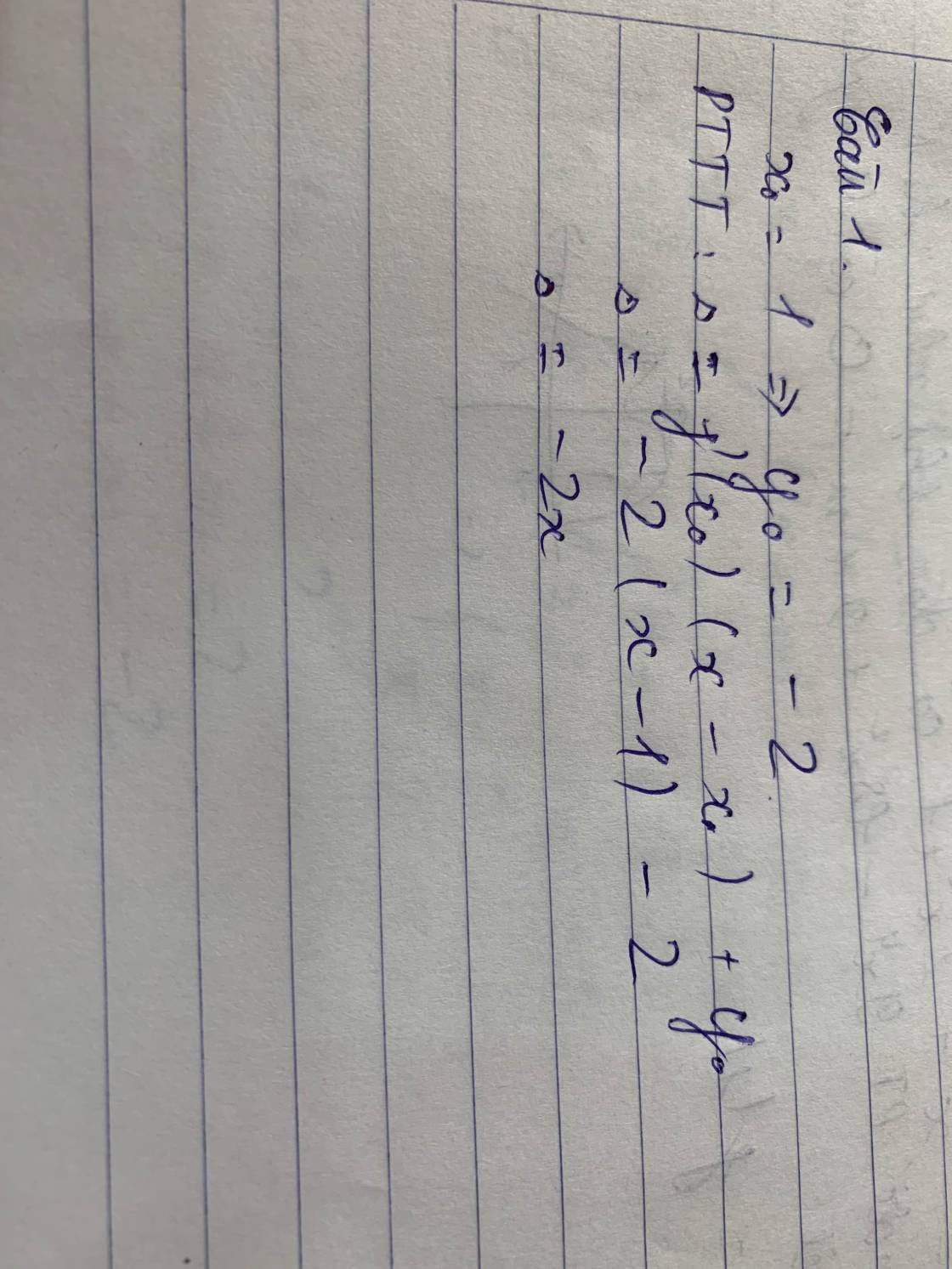
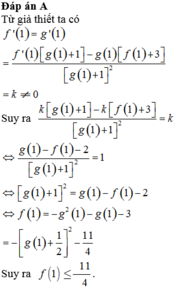
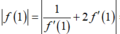
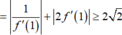
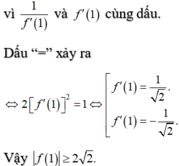
Câu 1:

\(f'\left(1\right)=g'\left(1\right)=k\)

\(h\left(x\right)=\frac{f\left(x\right)+2}{g\left(x\right)+1}\Rightarrow h'\left(x\right)=\frac{f'\left(x\right)\left[g\left(x\right)+1\right]-g'\left(x\right)\left[f\left(x\right)+2\right]}{\left[g\left(x\right)+1\right]^2}\)

\(\Rightarrow h'\left(1\right)=\frac{k\left(b+1\right)-k\left(a+2\right)}{\left(b+1\right)^2}=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\)

Mà \(h'\left(1\right)=k\Rightarrow k=\frac{k\left(b-a-1\right)}{\left(b+1\right)^2}\Rightarrow\frac{b-a-1}{\left(b+1\right)^2}=1\)

\(\Leftrightarrow b-a-1=\left(b+1\right)^2\Rightarrow a=b-1-\left(b+1\right)^2\)

\(\Rightarrow a=-b^2-b-2\)

Answer 2

[Nguyễn Việt Lâm]

Câu 2:

\(y=f\left(x\right)=\frac{x+1}{x-2}\Rightarrow f'\left(x\right)=\frac{-3}{\left(x-2\right)^2}\)

Phương trình hoành độ giao điểm:

\(\frac{x+1}{x-2}=x+m\Leftrightarrow x+1=\left(x+m\right)\left(x-2\right)\)

\(\Leftrightarrow x^2+\left(m-3\right)x-2m-1=0\)

\(\Delta=\left(m-3\right)^2+4\left(2m+1\right)=\left(m+1\right)^2+12>0\)

\(\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A và B có hoành độ giả sử là a và b

Theo Viet: \(\left\{{}\begin{matrix}a+b=3-m\\ab=-3m-1\end{matrix}\right.\) \(\Rightarrow3a+3b-ab=10\) (1)

Mặt khác do tiếp tuyến tại A và B song song

\(\Leftrightarrow\frac{-3}{\left(a-2\right)^2}=\frac{-3}{\left(b-2\right)^2}\Leftrightarrow\left[{}\begin{matrix}a-2=b-2\\a-2=2-b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4-b\end{matrix}\right.\)

TH1: \(a=b\) thay vào (1):

\(\Rightarrow-a^2+6a-10=0\left(vn\right)\)

TH2: \(a=4-b\)

\(\Rightarrow a+b=4\Rightarrow3-m=4\Rightarrow m=-1\)