Question

[Phạm Khánh Ly]

Câu 1. Tính giá trị của biểu thức:

P = \(\frac{2.3.4-2.3.4.9+2.3.4.11-2.3.4.13}{5.6.7-5.6.7.9+5.6.7.11-5.6.7.13}\)

Câu 2. Tính

A = \(\left(\frac{878787}{959595}+\frac{-8787}{9595}\right).\frac{1234321}{5678765}\)

Câu 3. Chứng minh rằng

S = \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}< 1\)

Câu 4. Một bác nông dân mang cam đi bán. Lần thứ nhất bán \(\frac{1}{2}\) số cam và 1/2 quả; lần thứ 2 bán 1/3 số cam còn lại và 1/3 quả. Cuối cùng còn lại 24 quả cam. Hỏi số cam bác nông dân đã mang đi bán?

Câu 5. So sánh

A = \(\frac{10^8+2}{10^8-1}\); B = \(\frac{10^8}{10^8-3}\)

Câu 6. CMR nếu

\(\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)⋮ 11 thì abcdeg ⋮ 11

Answer 1

[Nguyễn Thị Diễm Quỳnh]

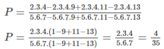
Câu 1 :

\(P=\frac{2.3.4-2.3.4.9+2.3.4.11-2.3.4.13}{5.6.7-5.6.7.9+5.6.7.11-5.6.7.13}\)

\(\Rightarrow P=\frac{2.3.4.\left(1-9+11-13\right)}{5.6.7\left(1-9+11-13\right)}=\frac{2.3.4}{5.6.7}=\frac{4}{35}\)

Câu 3 :

\(S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}< 1\)

\(\Rightarrow2S=2\left(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}\right)\)

\(S=1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{19}\)

Do đó : 2S - S = \(1-\frac{1}{2^{20}}\)

S = \(1-\frac{1}{2^{20}}\) < 1 (đpcm )

Answer 2

[Ngọc Lan Tiên Tử]

Câu 6 :

\(\overline{abcdeg}=\overline{ab}.10000+\overline{cd}.100+\overline{eg}\)

=\(\overline{ab}.9999+\overline{cd}.99+\left(\overline{ab}+\overline{cd}+\overline{eg}\right)\)

ta thấy :

\(\left[{}\begin{matrix}\overline{ab}.9999⋮11\\\overline{cd}.99⋮11\\\left(\overline{ab}+\overline{cd}+\overline{eg}\right)⋮11\end{matrix}\right.\)

( cái phần( \(\overline{ab}+\overline{cd}+\overline{eg}\))⋮11 theo đề bài )

=>\(\overline{abcdeg}⋮11\)