Cho các số x, y thỏa mãn 36x2+16y2\(=\)9. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P= -2x+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NT
1

22 tháng 11 2021
\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)
K
1

NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(\dfrac{3x^2-1}{x^2+2}=\dfrac{6x^2-2}{2\left(x^2+2\right)}=\dfrac{7x^2-\left(x^2+2\right)}{2\left(x^2+2\right)}=\dfrac{7x^2}{2\left(x^2+2\right)}-\dfrac{1}{2}\ge=-\dfrac{1}{2}\)
GTNN của biểu thức là \(-\dfrac{1}{2}\), xảy ra khi \(x=0\)
Biểu thức ko tồn tại GTLN

15 tháng 10 2021
\(A=139\)
\(\Leftrightarrow720:\left(x-6\right)=40\)
\(\Leftrightarrow x-6=18\)
hay x=24
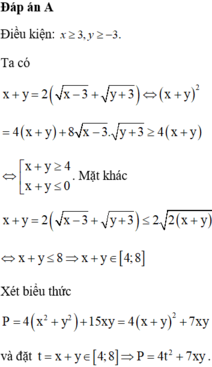
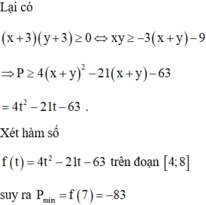
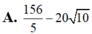
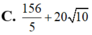



\(P^2=\left(-2x+y\right)^2=\left(\frac{-1}{3}.6x+\frac{1}{4}.4y\right)^2\)
\(\Rightarrow P^2\le\left[\left(-\frac{1}{3}\right)^2+\left(\frac{1}{4}\right)^2\right]\left[\left(6x\right)^2+\left(3y\right)^2\right]=\frac{13}{36}.\left(36x^2+16y^2\right)=\frac{13}{4}\)
\(\Rightarrow\frac{-\sqrt{13}}{2}\le P\le\frac{\sqrt{13}}{2}\)