Question

[Nguyễn Thanh]

Cho hàm số f(x) thỏa mản f(2) = -1/5 và f'(x) =x³ [f(x)]² với mọi x. tính giá trị f(1)?

Answer 1

[Nguyễn Linh Chi]

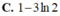
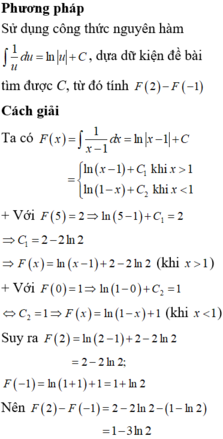
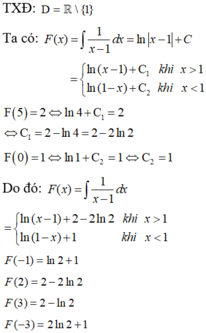
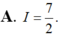
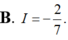
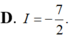
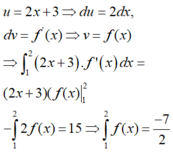
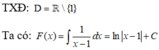
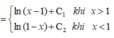
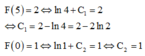
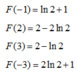
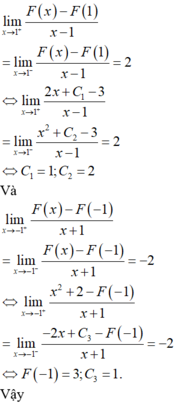
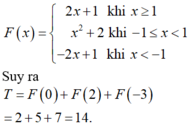
Ta có:

\(f'\left(x\right)=x^3\left[f\left(x\right)\right]^2\Leftrightarrow\frac{f'\left(x\right)}{\left[f\left(x\right)\right]^2}=x^3\)

Lấy nguyên hàm hai vế:

\(\int\frac{f'\left(x\right)}{\left[f\left(x\right)\right]^2}=\int x^3\Leftrightarrow-\frac{1}{f\left(x\right)}=\frac{x^4}{4}+C\)

f(2)=-1/5 <=> \(-\frac{1}{-\frac{1}{5}}=\frac{2^4}{4}+C\Leftrightarrow C=1\)

Suy ra: \(-\frac{1}{f\left(x\right)}=\frac{x^4}{4}+1\Leftrightarrow f\left(x\right)=-\frac{4}{x^4+4}\)

Answer 2

[Nguyễn Linh Chi]

Thay vào rồi tính đc f(1)