câu này khoai quá mn ơi làm 2 ngày chưa ra nữa, mn ai biết giải hộ mình mới
cho hàm số y =x4+ax3+bx2+1 đạt giá trọ nhỏ nhất =1, tính giá trị nhỏ nhất của a+b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Nó sẽ có tiệm cận ngang nếu giá trị x có thể tiến đến vô cùng và giới hạn khi x đến vô cùng phải tồn tại tức là a = 0 ; b > 0 . Với a , b ∈ Z thì a = 0 ; b = 1 ⇒ a + b = 1 .

Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
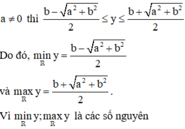
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
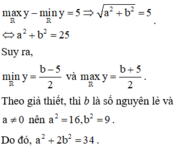

Tập xác định: D = R
Ta có
m a x x ∈ R f x = 4 ⇔ f x ≤ 4 ; ∀ x ∈ R ∃ x 0 ∈ R : f x 0 = 4 ⇔ a x + b x 2 + 1 ≤ 4 a x 0 + b x 2 0 + 1 = 4 ⇔ 4 x 2 - a x + 4 - b ≥ 0 4 x 0 2 - a x 0 + 4 - b = 0 ⇔ ∆ = a 2 + 16 b - 64 ≤ 0 ∆ = a 2 + 16 b - 64 ≥ 0 ⇔ a 2 + 16 b - 64 = 0 1
Đối với m i n x ∈ R f x = - 1 làm tương tự, ta đi đến a 2 - 4 b - 4 = 0 (2)
Giải hệ gồm (1) và (2) ta được a = ± 4 ; b = 3 .
Do n 2 + n + 2017 = n n + + 2017 là số lẻ ∀ n ∈ N nên a 2 + b 3 - 44 n 2 + n + 2017 = -1
Đáp án C
\(y'=4x^3+3ax^2+2bx\)
\(y'=0\Rightarrow x\left(4x^2+3ax+b\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x^2+3ax+b=0\end{matrix}\right.\)
Xét \(g\left(x\right)=4x^2+3ax+b=0\) với \(\Delta=9a^2-16b\)
Hàm số luôn có 1 cực trị là \(x=0\), với \(y\left(0\right)=1\)
Dựa vào hình dáng đồ thị hàm bậc 4, để \(y\) đạt GTNN bằng 1 cũng chính là \(y\left(0\right)\) ta có các trường hợp sau:
- TH1: \(\Delta\le0\Rightarrow9a^2-16b\le0\Rightarrow b\ge\frac{9a^2}{16}\)
Khi đó \(S=a+b\ge a+\frac{9a^2}{16}=\frac{9}{16}\left(a+\frac{8}{9}\right)^2-\frac{4}{9}\ge-\frac{4}{9}\)
- TH2: \(g\left(x\right)=0\) có 2 nghiệm cùng âm \(x_1< x_2< 0\) và \(y\left(x_1\right)=1\)
\(\Rightarrow\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\\frac{-3a}{4}< 0\\x_1^4+ax_1^3+bx_1^2+1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a>0\\x_1^2+ax_1+b=0\end{matrix}\right.\)
Nói chung ta ko cần tìm tiếp, do \(a;b>0\Rightarrow a+b>0>-\frac{4}{9}\)
TH3: \(g\left(x\right)=0\) có 2 nghiệm cùng dương \(0< x_1< x_2\) và \(y\left(x_2\right)=1\)
\(\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\-\frac{3a}{4}>0\\y\left(x_2\right)=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a< 0\end{matrix}\right.\)
\(y\left(x_2\right)=x_2^4+ax_2^3+bx_2^2+1=1\)
\(\Leftrightarrow x_2^2+ax_2+b=0\)
\(\Rightarrow\left\{{}\begin{matrix}4x_2^2+3ax_2+b=0\\x_2^2+ax_2+b=0\end{matrix}\right.\) \(\Rightarrow3x_2^2+2ax_2=0\Rightarrow x_2=-\frac{2a}{3}\)
\(\Rightarrow\frac{4a^2}{9}-\frac{2a^2}{3}+b=0\Rightarrow b=\frac{2a^2}{9}\)
\(\Rightarrow S=a+b=\frac{2a^2}{9}+a=\frac{2}{9}\left(a+\frac{9}{4}\right)^2-\frac{9}{8}\ge-\frac{9}{8}\)
So sánh 2 giá trị \(-\frac{4}{9}\) và \(-\frac{9}{8}\) ta được \(S_{min}=-\frac{9}{8}\) khi \(\left\{{}\begin{matrix}a=-\frac{9}{4}\\b=\frac{9}{8}\end{matrix}\right.\)