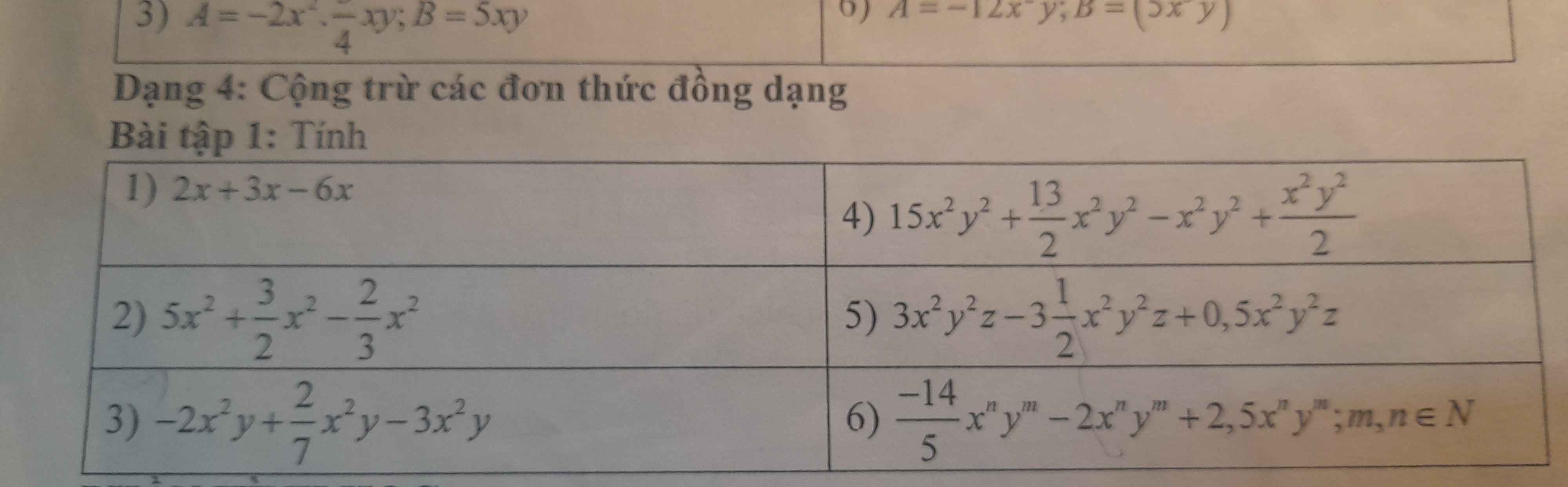giúp bài 4,5,6 với gập ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a. Khi $m=2$ thì hàm số là: $y=x+2$.
Cho $x=0$ thì $y=x+2=0+2=2$. Ta có điểm $(0,2)$
Cho $x=1$ thì $y=1+2=3$. Ta có điểm $(1,3)$
Nối $(0,2)$ với $(1,3)$ ta được đths $y=x+2$
b.
Để hàm đồng biến thì $m^2-3>0$
$\Leftrightarrow m> \sqrt{3}$ hoặc $m< -\sqrt{3}$
Để hàm nghịch biến thì $m^2-3<0$
$\Leftrightarrow -\sqrt{3}< m< \sqrt{3}$
c.
Để $(d)$ đi qua $A(1;2)$ thì:
$y_A=(m^2-3)x_A+2$
$\Leftrightarrow 2=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=3\Leftrightarrow m=\pm \sqrt{3}$
d. Để $(d)$ đi qua $B(1;8)$ thì:
$y_B=(m^2-3)x_B+2$
$\Leftrightarrow 8=(m^2-3).1+2=m^2-1$
$\Leftrightarrow m^2=9\Leftrightarrow m=\pm 3$
Bài 6:
$M$ nằm trên đường thẳng $2x+y=3$ nên:
$2x_M+y_M=3$
Mà $x_M=\frac{1}{2}$ nên $y_M=3-2x_M=3-2.\frac{1}{2}=2$
Vậy $M(\frac{1}{2};2)$
Gọi PTĐT $(d)$ là $y=ax+b$
$A(-2;1)\in (d)$ nên: $y_A=ax_A+b$
$\Rightarrow 1=-2a+b(1)$
$M(\frac{1}{2};2)\in (d)$ nên:
$y_M=ax_M+b$
$\Rightarrow 2=\frac{1}{2}a+b(2)$
Từ $(1); (2)\Rightarrow a=\frac{2}{5}; b=\frac{9}{5}$
$\Rightarrow (d): y=\frac{2}{5}x+\frac{9}{5}$

Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
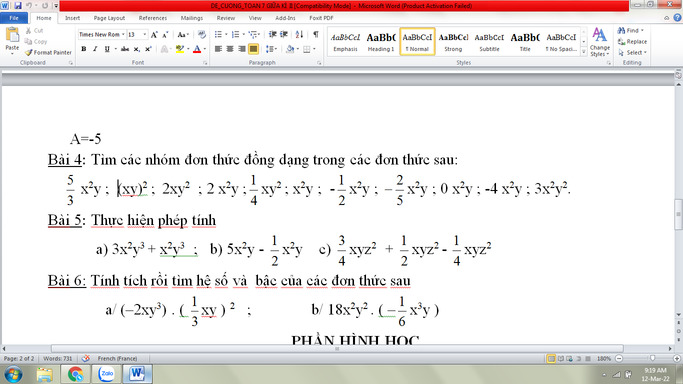
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)



Câu 4:
a) CTPT: CnH2n+2
\(n_{CO_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
=> \(n_{C_nH_{2n+2}}=\dfrac{0,25}{n}\left(mol\right)\)
=> \(M_{C_nH_{2n+2}}=\dfrac{3,6}{\dfrac{0,25}{n}}=14,4n\left(g/mol\right)\)
=> n = 5
=> CTPT: C5H12
CTCT:
(1) \(CH_3-CH_2-CH_2-CH_2-CH_3\) (pentan)
(2) \(CH_3-CH_2-CH\left(CH_3\right)-CH_3\) (2-metylbutan)
(3) \(\left(CH_3\right)_4C\) (2,2-đimetylpropan)
b) X tác dụng với clo thu được 1 sp thế duy nhất
=> X là (CH3)4C
Câu 5:
\(n_{Br_2}=\dfrac{24}{160}=0,15\left(mol\right)\)
=> \(n_{anken}=0,15\left(mol\right)\)
=> \(M_{anken}=\dfrac{8,4}{0,15}=56\left(g/mol\right)\)
=> X là C4H8
CTCT
(1) \(CH_2=CH-CH_2-CH_3\) (But-1-en)
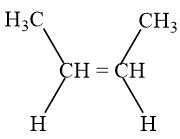
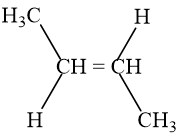
(2) \(CH_3-CH=CH-CH_3\) (But-2-en)
(3) \(\left(CH_3\right)_2C=CH_2\) (2-metylprop-1-en)
- đphh
(1) 
(2) 
b) X tác dụng với HCl chỉ thu được 1 sp
=> X là \(CH_3-CH=CH-CH_3\)
\(CH_3-CH=CH-CH_3+HCl\rightarrow CH_3-CH_2=CHCl-CH_3\)
Câu 6:
a)
C2H4 + Br2 --> C2H4Br2
C2H2 + 2Br2 --> C2H2Br4
\(C_2H_2+2AgNO_3+2NH_3\rightarrow C_2Ag_2\downarrow+2NH_4NO_3\)
b) TN1: Khí thoát ra khỏi bình là C2H6
=> \(V_{C_2H_6}=4,48\left(l\right)\)
TN2:
\(n_{C_2Ag_2}=\dfrac{36}{240}=0,15\left(mol\right)\)
=> \(n_{C_2H_2}=0,15\left(mol\right)\)
=> \(V_{C_2H_2}=0,15.22,4=3,36\left(l\right)\)
=> \(V_{C_2H_4}=11,2-4,48-3,36=3,36\left(l\right)\)

1, \(2x+3x-6x=-x\)
2, \(5x^2+\dfrac{3}{2}x^2-\dfrac{2}{3}x^2=\dfrac{35}{6}x^2\)
3, \(-2x^2y+\dfrac{2}{7}x^2y-3x^2y=-\dfrac{33}{7}x^2y\)
4, \(15x^2y^2+\dfrac{13}{2}x^2y^2-x^2y^2+\dfrac{x^2y^2}{2}=21x^2y^2\)
5, \(-\dfrac{14}{5}x^ny^m-2x^ny^m+2,5x^ny^m=-\dfrac{23}{10}x^ny^m\)
mình thiếu câu 5 :v câu 5 bài trước là câu 6 nhé
\(3x^2y^2z-\dfrac{7}{2}x^2y^2z+\dfrac{1}{2}x^2y^2z=0\)

Câu 4:
C1: Chúng ta
V1: chỉ nghĩ đến bản thân mình
C2: cả thế giới xung quanh
V2: chỉ còn là những chiếc bóng
=> kiểu câu xét theo ngữ pháp: Câu ghép
Câu 5:
Biện pháp điệp cấu trúc "Khi chúng ta..."
Tác dụng:
+ Tạo nhịp điệu nhanh dồn dập cho đoạn viết
+ Tác giả muôn cho người đọc thấy những tình huống khác nhau nếu chúng ta sống ích kỉ chỉ nghĩ đến bản thân
Câu 6:
Thông điệp tác giả muốn gửi tới chúng ta: sống cần có tình yêu thương với mọi người đừng ích kỉ, toan tính chỉ riêng cho bản thân ta. Vì:
- Con người luôn là một cá thể gắn với xã hội, nếu chúng ta cứ sống ích kỉ với nhau chẳng phải xã hội sẽ nhanh chóng trở thành mảnh đất chết của tình người giá băng
- Khi chúng ta trao đi yêu thương cũng là một cách yêu chính bản thân mình, tự đem lại niềm vui và sự an yên trong chính tâm hồn mình.

Để tính quãng đường đi được từ thời điểm t1 đến t2 cho vật giao động điều hòa dọc theo trục Ox, ta cần tính diện tích dưới đường cong x(t) trong khoảng thời gian từ t1 đến t2.
Trước tiên, chúng ta sẽ tính x(t) tại t1 và t2:
Tại t1 = 13/6 s: x(t1) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tại t2 = 23/6 s: x(t2) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tiếp theo, chúng ta cần tính diện tích dưới đường cong trong khoảng từ t1 đến t2. Để làm điều này, ta sẽ tính diện tích của hình giữa đồ thị và trục Ox trong khoảng từ t1 đến t2.
Diện tích A = ∫(t1 đến t2) x(t) dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - (3.14 / 3))] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(12.56 - 1.0467)] dt
A = ∫(13/6 đến 23/6) [3 * cos(11.5133)] dt
Giải tích phần này trở nên phức tạp, nhưng bạn có thể tính toán nó bằng máy tính hoặc phần mềm tính toán. Kết quả sẽ là diện tích A, tức là quãng đường đi được từ t1 đến t2.
(em thay pi=3,14 luôn nha anh )