|-2/5x - 1/5|-1/4=3/4 làm thế nào vậy ạ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\frac{1}{4}\right)^3+\frac{-3}{4}.|x-5|=\frac{-9}{2}\)
\(\Rightarrow\frac{1}{64}+\frac{-3}{4}.|x-5|=\frac{-9}{2}\)
\(\Rightarrow\frac{-3}{4}.|x-5|=\frac{-9}{2}-\frac{1}{64}\)
\(\Rightarrow\frac{-3}{4}.|x-5|=\frac{-289}{64}\)
\(\Rightarrow|x-5|=\frac{-289}{64}:\frac{-3}{4}\)
\(\Rightarrow|x-5|=\frac{289}{48}\)
\(\Rightarrow\orbr{\begin{cases}x-5=\frac{289}{48}\\x-5=\frac{-289}{48}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{529}{48}\\x=\frac{-49}{48}\end{cases}}\)
Vậy \(x=\frac{529}{48}\) hoặc \(x=\frac{-49}{48}\)

số các số hạng của dãy là :
( 100 - 1 ) : 1 + 1 = 100 ( số )
tổng của dãy đó là :
( 100 + 1 ) x 100 : 2 = 5050
ĐS:...
Số các số hạng là :
( 100 - 1 ) + 1 = 100 ( số )
Tổng của dãy số trên là :
( 100 + 1 ) x 100 : 2 = 5050
Đ/s : 5050

`@` `\text {Ans}`
`\downarrow`
`1)`
\(2x+\dfrac{1}{2}=\dfrac{5}{3}\)
`\Rightarrow`\(2x=\dfrac{5}{3}-\dfrac{1}{2}\)
`\Rightarrow`\(2x=\dfrac{7}{6}\)
`\Rightarrow`\(x=\dfrac{7}{6}\div2\)
`\Rightarrow`\(x=\dfrac{7}{12}\)
Vậy, `x = 7/12`
`2)`
\(\dfrac{1}{7}+\dfrac{4}{5}x=\dfrac{5}{3}\)
`\Rightarrow`\(\dfrac{4}{5}x=\dfrac{5}{3}-\dfrac{1}{7}\)
`\Rightarrow`\(\dfrac{4}{5}x=\dfrac{32}{21}\)
`\Rightarrow`\(x=\dfrac{32}{21}\div\dfrac{4}{5}\)
`\Rightarrow`\(x=\dfrac{40}{21}\)
Vậy, `x = 40/21`
`3)`
\(\dfrac{3}{5}-\dfrac{3}{5}x=\dfrac{1}{7}\)
`\Rightarrow`\(\dfrac{3}{5}x=\dfrac{3}{5}-\dfrac{1}{7}\)
`\Rightarrow`\(\dfrac{3}{5}x=\dfrac{16}{35}\)
`\Rightarrow`\(x=\dfrac{16}{35}\div\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{16}{21}\)
Vậy, `x = 16/21`
`4)`
\(\dfrac{5}{6}-3x=\dfrac{3}{4}\)
`\Rightarrow`\(3x=\dfrac{5}{6}-\dfrac{3}{4}\)
`\Rightarrow`\(3x=\dfrac{1}{12}\)
`\Rightarrow`\(x=\dfrac{1}{12}\div3\)
`\Rightarrow`\(x=\dfrac{1}{36}\)
Vậy, `x = 1/36`
`5)`
\(\dfrac{5}{3}-\dfrac{1}{2}x=\dfrac{3}{7}\)
`\Rightarrow`\(\dfrac{1}{2}x=\dfrac{5}{3}-\dfrac{3}{7}\)
`\Rightarrow`\(\dfrac{1}{2}x=\dfrac{26}{21}\)
`\Rightarrow`\(x=\dfrac{26}{21}\div\dfrac{1}{2}\)
`\Rightarrow`\(x=\dfrac{52}{21}\)
Vậy, `x = 52/21`
`6)`
\(5x+\dfrac{1}{2}=\dfrac{2}{3}\)
`\Rightarrow`\(5x=\dfrac{2}{3}-\dfrac{1}{2}\)
`\Rightarrow`\(5x=\dfrac{1}{6}\)
`\Rightarrow`\(x=\dfrac{1}{6}\div5\)
`\Rightarrow`\(x=\dfrac{1}{30}\)
Vậy, `x = 1/30.`

\(=5+\dfrac{2}{5}+4+\dfrac{3}{7}-\dfrac{1}{4}+\dfrac{4}{7}-2-\dfrac{2}{5}-\dfrac{3}{4}\)
\(=\left(5+4-2\right)+\left(\dfrac{2}{5}-\dfrac{2}{5}\right)+\left(\dfrac{3}{7}+\dfrac{4}{7}\right)-\dfrac{1}{4}-\dfrac{3}{4}\)
=7+1-1
=7

\(\left(x+2\right)-2=0\)
\(\Rightarrow x+2-2=0\)
\(\Rightarrow x=0\)
\(\left(x+3\right)+1=7\)
\(\Rightarrow x+3+1=7\)
\(\Rightarrow x+4=7\)
\(\Rightarrow x=3\)
\(\left(3x-4\right)+4=12\)
\(\Rightarrow3x-4+4=12\)
\(\Rightarrow3x=12\)
\(\Rightarrow x=4\)
\(\left(5x+4\right)-1=13\)
\(\Rightarrow5x+4-1=13\)
\(\Rightarrow5x+3=13\)
\(\Rightarrow5x=10\)
\(\Rightarrow x=2\)
\(\left(4x-8\right)-3=5\)
\(\Rightarrow4x-8-3=5\)
\(\Rightarrow4x-11=5\)
\(\Rightarrow4x=16\)
\(\Rightarrow x=4\)
\(8-\left(2x+4\right)=2\)
\(\Rightarrow8-2x-4=2\)
\(\Rightarrow4-2x=2\)
\(\Rightarrow2x=2\)
\(\Rightarrow x=1\)
\(7+\left(5x+2\right)=14\)
\(\Rightarrow7+5x+2=14\)
\(\Rightarrow9+5x=14\)
\(\Rightarrow5x=5\)
\(\Rightarrow x=1\)
\(5-\left(3x-11\right)=1\)
\(\Rightarrow5-3x+11=1\)
\(\Rightarrow16-3x=1\)
\(\Rightarrow3x=15\)
\(\Rightarrow x=5\)


Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
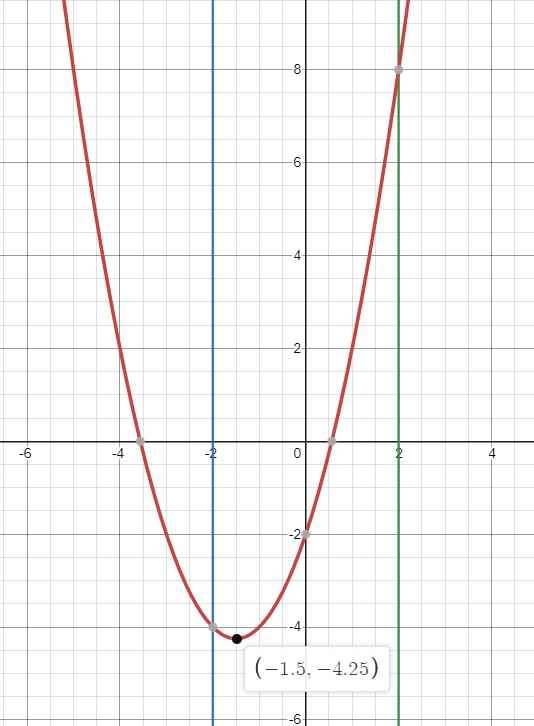
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
thầy cho em hỏi làm mấy dạng tìm điều kiện này thạo thì nên học qua tư liệu nào ? Thầy có thể cho e một số file chuyên đề về mấy dạng này đc không?

\(\left|-\frac{2}{5}x-\frac{1}{5}\right|-\frac{1}{4}=\frac{3}{4}\)
\(\Leftrightarrow\left|-\frac{2}{5}x-\frac{1}{5}\right|=\frac{3}{4}+\frac{1}{4}\)
\(\Leftrightarrow\left|-\frac{2}{5}x-\frac{1}{5}\right|=\frac{4}{4}\)
\(\Leftrightarrow\left|-\frac{2}{5}x-\frac{1}{5}\right|=1\)
\(\Leftrightarrow\orbr{\begin{cases}-\frac{2}{5}x-\frac{1}{5}=1\\-\frac{2}{5}x-\frac{1}{5}=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)
Vậy x = -3 hoặc x = 2
\(\left|-\frac{2}{5}x-\frac{1}{5}\right|-\frac{1}{4}=\frac{3}{4}\)
=> \(\left|-\frac{2}{5}x-\frac{1}{5}\right|=1\)
=> \(\orbr{\begin{cases}-\frac{2}{5}x-\frac{1}{5}=1\\-\frac{2}{5}x-\frac{1}{5}=-1\end{cases}}\)
=> \(\orbr{\begin{cases}-\frac{2}{5}x=\frac{6}{5}\\-\frac{2}{5}x=-\frac{4}{5}\end{cases}}\)
=> \(\orbr{\begin{cases}x=-3\\x=2\end{cases}}\)