Cho hình chóp S.ABCD có SA⊥(ABCD),SA⊥(ABCD), đáy ABCD là hình vuông,M là trung điểm AB .Tìm khoảng cách của SB giữa...
Đọc tiếp
Cho hình chóp S.ABCD có SA⊥(ABCD),SA⊥(ABCD), đáy ABCD là hình vuông,M là trung điểm AB .Tìm khoảng cách của SB giữa CM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
19 tháng 11 2021
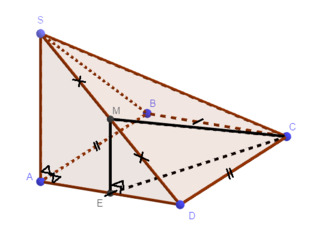
Gọi E là trung điểm AD, ta có: ME//SA (ME là đường trung bình tam giác SAD) và SA, CE chéo nhau; suy ra (MCE) vuông góc (ABCD) và không chứa SA; suy ra SA//(MCE). Suy ra, d(SA,CM) = d(SA,(MCE)) = d(A,(MCE)) = d(D,(MCE)) = d(D,EC) = ED.DC/EC = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
HN
19 tháng 11 2021
Xin lỗi, mình sửa lại bài giải.
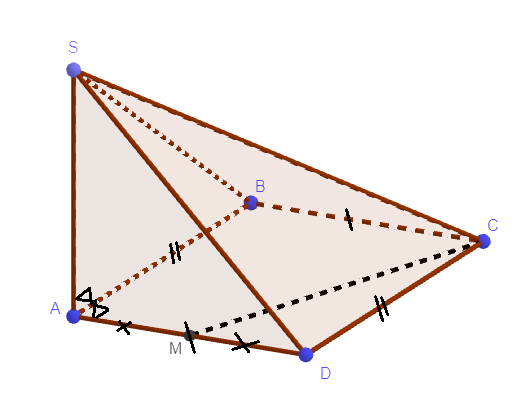
d(SA,CM) = d(A,CM) = d(D,CM) = MD.DC/CM = a.3a/a\(\sqrt{10}\) = 3a\(\sqrt{10}\)/10.
CM
7 tháng 2 2017
Đáp án là D
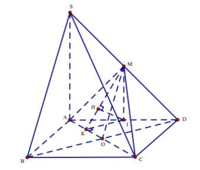
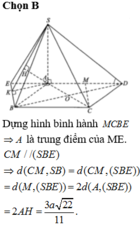
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác
CM
30 tháng 6 2019
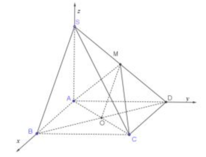
Chọn B.
Phương pháp:
Gắn hệ trục tọa độ.
Cách giải:
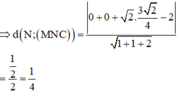
Vây, khoảng cách từ N đến mặt phẳng (MCD) bằng: 1 4 a
17 tháng 6 2023
1: SA vuông góc (ABCD)
=>SA vuông góc AB
=>ΔSAB vuông tại A
SA vuông góc (ABCD)
=>SA vuông góc AD
=>ΔSAD vuông tại A
4: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ
(SC;(ABCD))=(CS;CA)=góc SCA
AC=căn a^2+a^2=a*căn 2
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
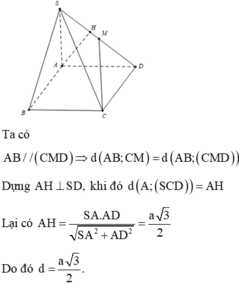
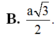
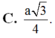
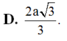
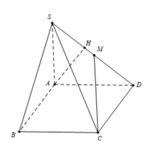
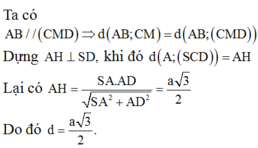
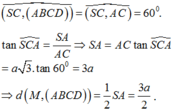
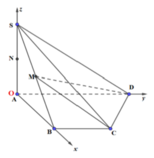
Đề bài thiếu tất cả các dữ liệu về độ dài (cạnh hình vuông đáy, độ dài SA...) cho nên mình nêu hướng giải, bạn tự điền
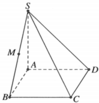
Gọi cạnh hình vuông là \(x\)
Gọi N là trung điểm SA \(\Rightarrow NM//SB\) (đường trung bình)
\(\Rightarrow SB//\left(CMN\right)\Rightarrow d\left(SB;CM\right)=d\left(SB;\left(CMN\right)\right)=d\left(S;\left(CMN\right)\right)\)
Mà SA cắt \(\left(CMN\right)\) tại N, \(SN=AN\) (N là trung điểm)
\(\Rightarrow d\left(S;\left(CMN\right)\right)=d\left(A;\left(CMN\right)\right)\)
Từ A kẻ \(AH\perp CM\Rightarrow CM\perp\left(SAH\right)\)
Từ A kẻ \(AK\perp NH\Rightarrow AK\perp\left(CMN\right)\Rightarrow AK=d\left(A;\left(CMN\right)\right)\)
\(CM=\sqrt{BC^2+BM^2}=\sqrt{x^2+\left(\frac{x}{2}\right)^2}=\frac{x\sqrt{5}}{2}\)
\(AH=AM.sin\widehat{HMA}=\frac{AB}{2}.\frac{BC}{CM}=\frac{x\sqrt{5}}{5}\)
\(NA=\frac{SA}{2}=...\)
\(\frac{1}{AK^2}=\frac{1}{NA^2}+\frac{1}{AH^2}\Rightarrow AK=\frac{NA.AH}{\sqrt{NA^2+AH^2}}=...\)