Cho d song song d', 1 cát tuyến cắt d,d' tại M,N. Qua O trung điểm M,N kẻ 1 cát tuyến cắt d và d' ở P,Q.
a) Chứng minh PM=NQ
b) Chứng minh PN song song MQ và PN=MQ
Các bạn giải nhanh giúp mk với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 11 2016
Có phải cát tuyến của hai đường tròn đi qua A không bạn nhỉ?
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 1 2018
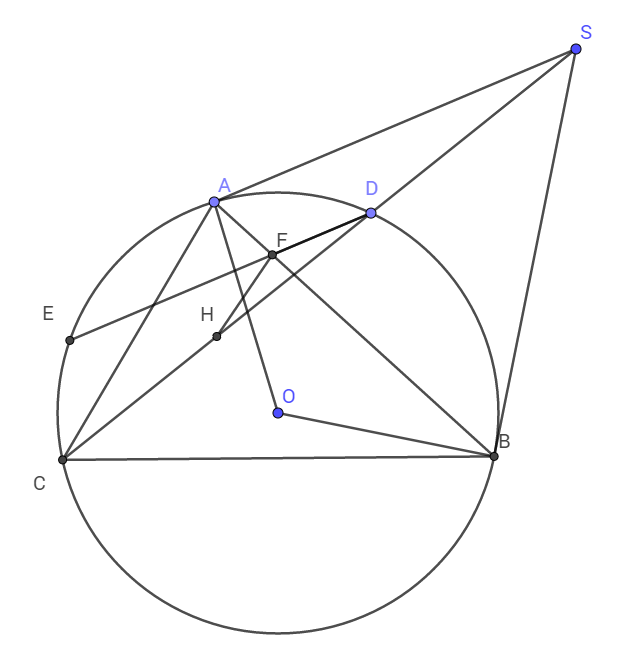
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.
27 tháng 6 2020
câu a;b em giải được rồi còn câu cd thôi. mọi người giúp đỡ
LM
6 tháng 3 2022
b, tam giác MCB ~ tam giác MBA (g.g) => BC/BA =MC/MD (vì MB=MD <= t/c 2 tiếp tuyến cắt nhau) (1)
tam giác MCD ~ tam giác MDA (g.g) => MC/MD= DC/AD (2)
Từ (1),(2) => BC/BA = DC/AD => BC.AD = DC.AB (đpcm)
CM
18 tháng 1 2018
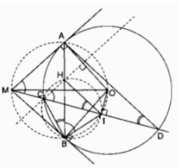
A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
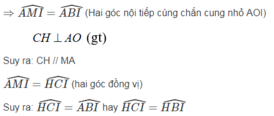
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.
