Giúp mk vs ạ <3
Cho x,y,z dương thỏa mãn : xy+yz+zx=xyz
CHỨNG MINH: (x^2y/y+2x) + (y^2z/z+2y)+ (z^2x/x+2z) >9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)

=>x(y-3)+3(y-3)=17
=>(y-3)(x+3)=17
\(\Leftrightarrow\left(x+3,y-3\right)\in\left\{\left(1;17\right);\left(17;1\right);\left(-1;-17\right);\left(-17;-1\right)\right\}\)
hay \(\left(x,y\right)\in\left\{\left(-2;20\right);\left(14;4\right);\left(-4;-14\right);\left(-20;2\right)\right\}\)


b:
=>x(y-3)+3(y-3)=17
=>(y-3)(x+3)=17
\(\Leftrightarrow\left(x+3,y-3\right)\in\left\{\left(1;17\right);\left(17;1\right);\left(-1;-17\right);\left(-17;-1\right)\right\}\)
hay \(\left(x,y\right)\in\left\{\left(-2;20\right);\left(14;4\right);\left(-4;-14\right);\left(-20;2\right)\right\}\)
a: =>x(2y+3)+2(2y+3)=5
=>(2y+3)(x+2)=5
\(\Leftrightarrow\left(2y+3;x+2\right)\in\left\{\left(1;5\right);\left(-1;-5\right);\left(5;1\right);\left(-5;-1\right)\right\}\)
hay \(\left(y,x\right)\in\left\{\left(-1;3\right);\left(-2;-7\right);\left(1;-1\right);\left(-4;-3\right)\right\}\)

ĐKXĐ: \(x\ge3\)
\(\Leftrightarrow\sqrt{x-3}=2\sqrt{x^2-9}\)
\(\Leftrightarrow x-3=4\left(x-3\right)\left(x+3\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\4\left(x+3\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{11}{4}\left(loại\right)\end{matrix}\right.\)

Mai Anh tính sai rồi nha bạn dù kết quả của bạn vẫn đúng nha
27^150 = (3^3)^150 = 3^450
9^226= (3^2)^226 = 3^452
Mà 3^452 > 3^450 suy ra 9^226 > 27^150

A=(-3/4+2/3).11/9+(-1/4+1/3):|-9/11|
\(=\left(-\frac{3}{4}+\frac{2}{3}\right).\frac{11}{9}+\left(-\frac{1}{4}+\frac{1}{3}\right).\frac{11}{9}\)
\(=\frac{11}{9}\left(-\frac{3}{4}+\frac{2}{3}-\frac{1}{4}+\frac{1}{3}\right)\)
\(=\frac{11}{9}\left(-1+1\right)\)
\(=\frac{11}{9}.0\)
=0

Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
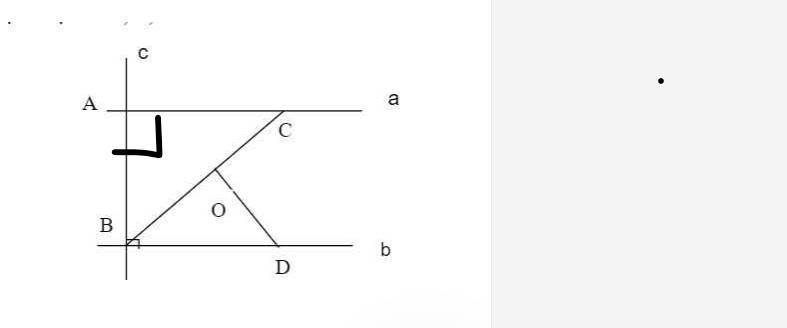
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC
Có \(xy+yz+zx=xyz\)\(\Leftrightarrow\)\(\frac{xy+yz+zx}{xyz}=1\)\(\Leftrightarrow\)\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1\)
\(\frac{x^2y}{y+2x}+\frac{y^2z}{z+2y}+\frac{z^2x}{x+2z}=\frac{1}{\frac{1}{x^2}+\frac{2}{xy}}+\frac{1}{\frac{1}{y^2}+\frac{2}{yz}}+\frac{1}{\frac{1}{z^2}+\frac{2}{zx}}\ge\frac{9}{\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}+2\left(\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}\right)}\)
\(=\frac{9}{\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^2}=\frac{9}{1^2}=9\)
Dấu "=" ko xảy ra \(\Rightarrow\)\(\frac{x^2y}{y+2x}+\frac{y^2z}{z+2y}+\frac{z^2x}{x+2z}>9\)