Tìm tích P tất cả các giá trị của m để phương trình 3x2+(2-m)x+m+1=0 có nghiệm kép .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2018
Phương trình có hai nghiệm phân biệt ⇔ ∆ > 0
⇔ m 2 - 8 m + 16 = 0 m - 4 2 > 0 ⇔ m ≠ 4 *
Theo định lí Viet, ta có:
x 1 . x 2 = m − 1 3 ; x 1 + x 2 = m + 2 3 x 1 = 2 x 2 ⇔ x 1 = 2 9 ( m + 2 ) , x 2 = 1 9 ( m + 2 ) x 1 . x 2 = m − 1 3
⇒ 2 81 ( m + 2 ) 2 = m − 1 3 ⇔ 2 m 2 − 19 m + 35 = 0 ⇔ m = 5 2 m = 7 (thỏa mãn (*))
Đáp án cần chọn là: A
CM
11 tháng 1 2017
Đáp án A
Em có x 3 − 3 x 2 − m = 0 ⇔ x 3 − 3 x 2 = m
Khi đó yêu cầu đầu bài tương đương với đồ thị hàm số y = x 3 − 3 x 2 cắt đường thẳng y = m tại 3 điểm trong đó có 2 điểm có hoành độ lớn hơn 1. Em có đồ thị hàm số y = x 3 − 3 x 2 như hình bên.
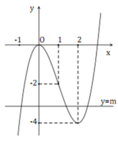
Từ đồ thị em thấy − 4 < m < − 2
CM
20 tháng 2 2017
Đáp án A
Xét hàm số f x = x 4 − 3 x 2 ,
có f ' x = 4 x 3 − 6 x = 0 ⇔ x = 0 x = ± 6 2 .
Tính các giá trị f 0 = 0 ; f ± 6 2 = − 9 4
=> Đồ thị (C) của hàm số y=f(x) .
Để phương trình f x = m + 1 có 2 nghiệm phân biệt
⇔ m + 1 > 0 m + 1 = − 9 4 ⇔ m > − 1 m = − 13 4
CM
25 tháng 6 2017
Đáp án B
Ta có:
x 3 − 3 x 2 + m x + 2 − m = 0 ⇔ x − 1 x 2 − 2 x + m − 2 = 0 ⇔ x = 1 x 2 − 2 x + m − 2 = 0 2
(2) có 2 nghiệm nếu = 1 − m − 2 ≥ 0 ⇔ m ≤ 3 .
Khi đó 2 nghiệm là:
x 1 = 1 + 3 − m ; x 2 = 1 − 3 − m
Ta thấy 3 giá trị 1 + 3 − m ; 1 ; 1 − 3 − m theo thứ tự luôn lập thành một cấp số cộng.
Vậy m ≤ 3
CM
28 tháng 11 2019
Phương trình có hai nghiệm phân biệt ⇔ ∆ ' > 0
⇔ m 2 - 7 m + 16 > 0 ⇔ m − 7 2 2 + 15 4 > 0 , ∀ m ∈ R
Theo định lí Viet, ta có:
x 1 . x 2 = 3 m − 5 3 ; x 1 + x 2 = 2 ( m + 1 ) 3 x 1 = 3 x 2 ⇔ x 1 = m + 1 2 , x 2 = m + 1 6 x 1 . x 2 = 3 m − 5 3
⇒ m + 1 2 12 = 3 m − 5 3 ⇔ m 2 − 10 m + 21 = 0 ⇔ m = 3 m = 7
Đáp án cần chọn là: C
8 tháng 5 2021
phương trình có nghiệm khi:
\(\Delta\)\(\ge\)0<=>[-(2m+1)]^2-4.(m^2-1)\(\ge\)0
<=>(2m+2)^2-4m^2+4\(\ge\)0
<=>4m^2+8m+4-4m^2+4\(\ge\)0
<=>8m+8\(\ge\)0
<=>8(m+1)\(\ge\)0
<=>m\(\ge\)-1
vậy m\(\ge\)-1 thì phương trình có nghiệm
8 tháng 5 2021
△≥0⇔(2m+2)^2-4(m^2-1)≥0
⇔4m^2+8m+4-4m^2+4≥0
⇔8m+8≥0
⇔m≥-1
Vậy phương trình có nghiệm khi m≥-1
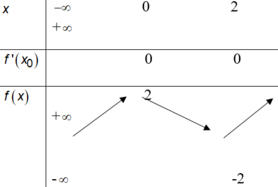
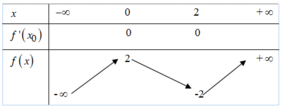
\(\Delta=\left(2-m\right)^2-12\left(m+1\right)=m^2-16m-8\)
Để phương trình có nghiệm kép
\(\Leftrightarrow\Delta=0\Leftrightarrow m^2-16m-8=0\) (1)
Do \(ac=-8< 0\) nên (1) luôn có 2 nghiệm
Theo Viet ta có: \(P=m_1m_2=-8\)