Cho hàm số f(x)=(x\(^2\)+2*x)*\(\sqrt{x-1}\) .Giải bất phương trình f ' (x) >=0
M.n giải hộ mình câu này với ạ.Cảm ơn mn nhiều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:f'(x)=4x-1
=>f'(x)\(\sqrt{x^2+1}=2x^2+2x+1\)
<=>(4x-1)\(\sqrt{x^2+1}=2x^2+2x+1\)
Nhận xét: vế phải > 0 nên đk để phương trình có nghiệm:x>\(\dfrac{1}{4}\)
Từ điều kiện trên phương trình
<=>(16x2-8x+1)(x2+1)=4x4+8x3+8x2+4x+1
<=>16x4+16x2-8x3-8x+x2+1=4x4+8x3+8x2+4x+1
<=>12x4-16x3+9x2-12x=0
<=>x(12x3-16x2+9x-12)=0
<=>x(3x-4)(4x2+3)=0
<=>x=0 hoặc x=\(\dfrac{4}{3}\)(do 4x2+3>0)
Vậy...

Đáp án D
Đồ thị hàm số y = f ( x ) = x 3 - 3 x + 1 có dạng:
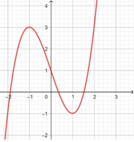
Dựa vào đồ thị ta thấy phương trình f(x) =0 có 3 nghiệm


![]()
Quan sát bảng biến thiên ta thấy phương trình này có 2 nghiệm.
Chọn D

Đáp án A
Ta có
![]()
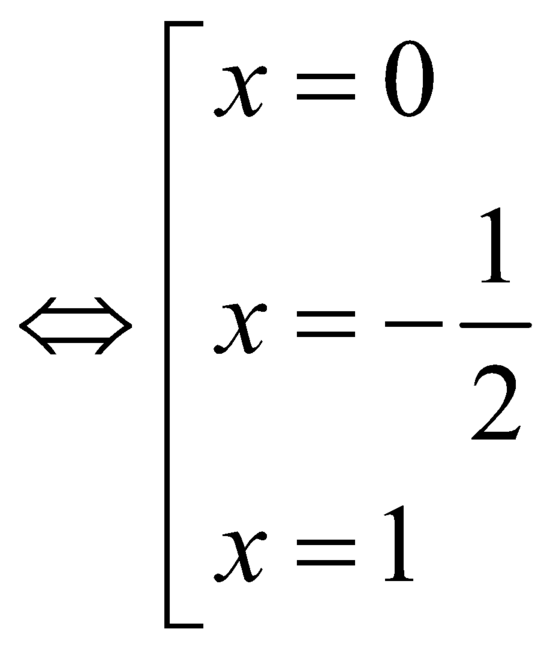 .
.
Bảng xét dấu:
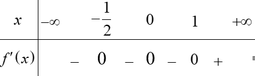
Suy ra hàm số có một điểm cực trị.

a) \(\frac{2-x}{3}< \frac{3-2x}{5}\)
<=> \(10-5x< 9-6x\)
<=> x < - 1
Vậy S = { x| x < -1 }
b)
0 -1
\(x>1\)
\(f'\left(x\right)=\left(2x+2\right)\sqrt{x-1}+\frac{x^2+2x}{2\sqrt{x-1}}=\frac{5x^2+2x-4}{2\sqrt{x-1}}\)
\(f'\left(x\right)\ge0\Leftrightarrow\frac{5x^2+2x-4}{\sqrt{x-1}}\ge0\Leftrightarrow5x^2+2x-4\ge0\)
\(\Rightarrow x>1\)
Mình k hiểu bước đầu lắm.Bạn giải thích hộ mình với