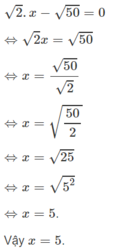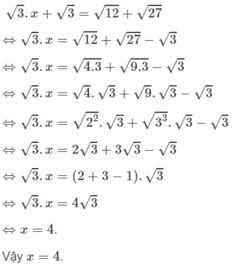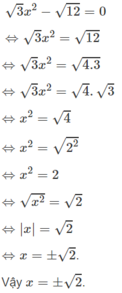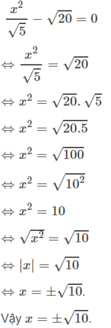x2_ (m_4)x _m +3=0. Tìm m để x15 +x25 =31
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 12 2021
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=a\\x_1x_2=1\end{matrix}\right.\)
\(A=x_1^5+x_2^5=\left(x_1^2+x_2^2\right)\left(x_1^3+x_2^3\right)-x_1^2x_2^2\left(x_1+x_2\right)\\ \Leftrightarrow A=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\left[\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)\right]-a\\ \Leftrightarrow A=\left(a^2-2\right)\left(a^3-3a\right)-a\\ \Leftrightarrow A=a^5-5a^3+5a\)
CD
3
HA
0
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
\(y'=\dfrac{-3-m}{\left(x-1\right)^2}\) ; \(y\left(2\right)=m+5\) ; \(y'\left(2\right)=-m-3\)
Phương trình tiếp tuyến tại điểm có hoành độ \(x=2\):
\(y=\left(-m-3\right)\left(x-2\right)+m+5\)
\(\Leftrightarrow y=-\left(m+3\right)x+3m+11\)
Để tiếp tuyến cắt 2 trục tạo thành tam giác \(\Rightarrow m\ne\left\{-3;-\dfrac{11}{3}\right\}\)
Gọi A và B lần lượt là giao điểm của tiếp tuyến với Ox và Oy
\(\Rightarrow A\left(\dfrac{3m+11}{m+3};0\right)\) ; \(B\left(0;3m+11\right)\)
\(\Rightarrow OA=\left|\dfrac{3m+11}{m+3}\right|\) ; \(OB=\left|3m+11\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{25}{2}\Rightarrow\dfrac{\left(3m+11\right)^2}{\left|m+3\right|}=25\)
\(\Leftrightarrow\left(3m+11\right)^2=25\left|m+3\right|\Rightarrow\left[{}\begin{matrix}\left(3m+11\right)^2=-25\left(m+3\right)\\\left(3m+11\right)^2=25\left(m+3\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}9m^2+91m+196=0\\9m^2+41m+46=0\end{matrix}\right.\) \(\Rightarrow m=...\)
26 tháng 11 2021
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Y
2
5 tháng 2 2021
\(a,\left(-31\right).\left(x+7\right)=0\\ \Rightarrow x+7=0\\ \Rightarrow x=-7\\ b,\left(8-x\right).\left(x+13\right)=0\\ \Rightarrow\left[{}\begin{matrix}8-x=0\\x+13=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-13\end{matrix}\right.\\ c,\left(x^2-25\right)\left(3-x\right)=0\\ \Rightarrow\left(x-5\right)\left(x+5\right)\left(3-x\right)=0\\\Rightarrow \left[{}\begin{matrix}x-5=0\\x+5=0\\3-x=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\x=-5\\x=3\end{matrix}\right.\\ d,\left(x-3\right)\left(x^2+4\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-3=0\\x^2+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x^2=-4\left(loại\right)\end{matrix}\right.\\ \Rightarrow x=3\)