Chứng tỏ 2^0+2^1+2.(2^2+2^3+...+2^9+2^10)+2^11+2^12 chia hết cho 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
LM
0

NM
1

16 tháng 8 2022
b: \(=2^{11}\left(1+2\right)=2^{11}\cdot3⋮3\)
c: \(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^7\left(1+2\right)\)
\(=3\left(2+2^3+...+2^7\right)⋮3\)
LY
0

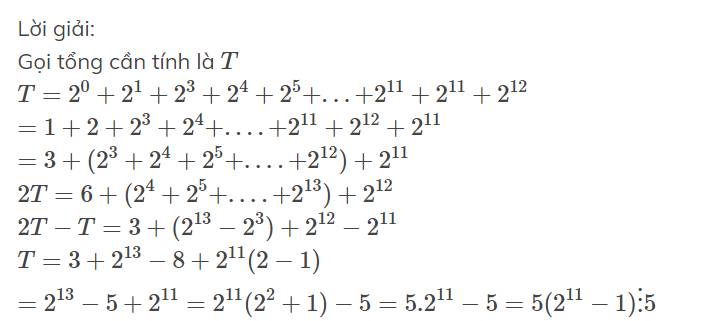
Lời giải:
Gọi tổng cần tính là $T$
$T=2^0+2^1+2^3+2^4+2^5+...+2^{11}+2^{11}+2^{12}$
$=1+2+2^3+2^4+....+2^{11}+2^{12} + 2^{11}$
$=3+(2^3+2^4+2^5+....+2^{12})+2^{11}$
$2T=6+(2^4+2^5+....+2^{13})+2^{12}$
$2T-T=3+(2^{13}-2^3)+2^{12}-2^{11}$
$T=3+2^{13}-8+2^{11}(2-1)$
$=2^{13}-5+2^{11}=2^{11}(2^2+1)-5=5.2^{11}-5=5(2^{11}-1)\vdots 5$