Rút gọn biểu thức
A= 4sin2α/1 - cos2(a/2)
B= (1 + cosα - sinα)/ (1- cosα - sinα)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2

a/ \(A=\left(sin\alpha+cos\alpha\right)^2+\left(sin\alpha-cos\alpha\right)^2=2\left(sin^2\alpha+cos^2\alpha\right)=2\)
b/ \(B=\left(1+tan^2\alpha\right)\left(1-sin^2\alpha\right)-\left(1+cotg^2\alpha\right)\left(1-cos^2\alpha\right)\)
\(=\left(1+\frac{sin^2\alpha}{cos^2\alpha}\right)\left(1-sin^2\alpha\right)-\left(1+\frac{cos^2\alpha}{sin^2\alpha}\right)\left(1-cos^2\alpha\right)\)
\(=\frac{1}{cos^2\alpha}.cos^2\alpha-\frac{1}{sin^2\alpha}.sin^2\alpha=1-1=0\)

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)

\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)

Đáp án: A
Vì tanα = 3/5 nên cosα ≠ 0, chia tử và mẫu của biểu thức cho cosα, ta được:
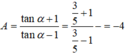

$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.
\(A=\frac{4sin2a}{1-2cos^2\frac{a}{2}}=\frac{4\left(2sina.cosa\right)}{1-\left(1+cosa\right)}=\frac{8sina.cosa}{-cosa}=-8sina\)
\(B=\frac{1+cosa-sina}{1-cosa-sina}=\frac{1+2cos^2\frac{a}{2}-1-2sin\frac{a}{2}cos\frac{a}{2}}{1-\left(1-2sin^2\frac{a}{2}\right)-2sin\frac{a}{2}cos\frac{a}{2}}=\frac{2cos^2\frac{a}{2}-2sin\frac{a}{2}cos\frac{a}{2}}{2sin^2\frac{a}{2}-2sin\frac{a}{2}cos\frac{a}{2}}\)
\(=\frac{-cos\frac{a}{2}\left(2sin\frac{a}{2}-2cos\frac{a}{2}\right)}{sin\frac{a}{2}\left(2sin\frac{a}{2}-2cos\frac{a}{2}\right)}=\frac{-cos\frac{a}{2}}{sin\frac{a}{2}}=-cot\frac{a}{2}\)