K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 8 2023
a: \(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
=>(SAD) giao (SBC)=xy, xy đi qua S, xy//AD//BC
b: Chọn mp(SBC) có chứa BC
\(P\in SC\subset\left(SBC\right)\)
\(P\in\left(MNP\right)\)
=>\(P\in\left(MNP\right)\cap\left(SBC\right)\)
mà NP//SB
nên (MNP) giao (SBC)=xy, xy đi qua P và xy//NP//SB
=>(MNP) giao (SBC)=PN
Gọi I là giao của PN với BC
=>I trùng với N
28 tháng 8 2023
a: \(I\in AC\subset\left(SAC\right)\)
\(I\in BD\subset\left(SBD\right)\)
Do đó: \(I\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SI\)
b: \(SD\subset\left(SCD\right)\)
\(SD\subset\left(SAD\right)\)
Do đó: \(SD=\left(SCD\right)\cap\left(SAD\right)\)
c: \(K\in SD\subset\left(SAD\right)\)
\(K\in\left(KAB\right)\)
Do đó: \(K\in\left(KAB\right)\cap\left(SAD\right)\)
mà \(A\in\left(AKB\right)\cap\left(SAD\right)\)
nên \(\left(KAB\right)\cap\left(SAD\right)=KA\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
a.
Trong mp (ABCD), kéo dài AD và BC cắt nhau tại E
\(\left\{{}\begin{matrix}E\in AD\in\left(SAD\right)\\E\in BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(SAD\right)\cap\left(SBC\right)\)
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
b.
Gọi O là giao điểm AC và BD \(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Trong mp (SBD), nối DM cắt SO tại I
\(\left\{{}\begin{matrix}I\in SO\in\left(SAC\right)\\I\in DM\end{matrix}\right.\)
\(\Rightarrow I=DM\cap\left(SAC\right)\)
c.
Gọi F là trung điểm SA \(\Rightarrow FM\) là đường trung bình tam giác SAB
\(\Rightarrow FM||AB\Rightarrow FM||CD\)
Mà \(M\in\left(MCD\right)\Rightarrow F\in\left(MCD\right)\)
\(\Rightarrow\) Tứ giác CDFM là thiết diện của (MCD) và chóp
CM
3 tháng 1 2020
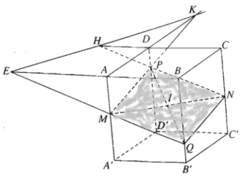
a) Ta có mặt phẳng (AA', DD') song song với mặt phẳng (BB', CC'). Mặt phẳng (MNP) cắt hai mặt phẳng nói trên theo hai giao tuyến song song.
Nếu gọi Q là điểm trên cạnh BB' sao cho NQ // PM thì Q là giao điểm của đường thẳng BB' với mặt phẳng (MNP)
Nhận xét. Ta có thể tìm điểm Q bằng cách nối P với trung điểm I của đoạn MN và đường thẳng PI cắt BB' tại Q.
b) Vì mặt phẳng (AA', BB') song song với mặt phẳng (DD', CC') nên ta có MQ // PN. Do đó mặt phẳng (MNP) cắt hình hộp theo thiết diện MNPQ là một ình bình hành.
Giả sử P không phải là trung điểm của đoạn DD'. Gọi H = PN ∩ DC , K = MP ∩ AD. Ta có D = HK là giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
Chú ý rằng giao điểm E = AB ∩ MQ cũng nằm trên giao tuyến d nói trên. Khi P là trung điểm của DD' mặt phẳng (MNP) song song với mặt phẳng (ABCD).
M
27 tháng 8 2023
a) Trong hình chóp S.MNP, các thành phần được kể tên như sau:
Đỉnh: SCác cạnh bên: SM, SN, SPCạnh đáy: MNPMặt bên: Các mặt tam giác SMN, SNP, SMPMặt đáy: Tam giác MNPb) Để tìm giao tuyến của hai mặt phẳng (SMN) và (MNP), chúng ta cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa đường chéo của tam giác MNP, vì đường chéo của tam giác nằm trên mặt phẳng (SMN) và (MNP) cùng một lúc.
c) Để tìm giao tuyến của hai mặt phẳng (SMP) và (SNP), chúng ta cũng cần tìm đường thẳng giao của hai mặt phẳng này. Đường thẳng này chính là đường thẳng chứa cạnh SP của tam giác SNP và cạnh SP của tam giác SMP, vì cả hai cạnh này nằm trên mặt phẳng (SMP) và (SNP) cùng một lúc.
6 tháng 9 2023
a: Đỉnh: S
Cạnh bên: SM,SN,SP
Cạnh đáy: MN,MP,NP
Mặt bên: SNP,SMP,SNM
Mặt đáy: MNP
b: \(MN\subset\left(SMN\right)\)
\(MN\subset\left(MNP\right)\)
Do đó: \(\left(SMN\right)\cap\left(MNP\right)=MN\)
c: \(SP\subset\left(SMP\right)\)
\(SP\subset\left(SNP\right)\)
Do đó: \(\left(SMP\right)\cap\left(SNP\right)=SP\)