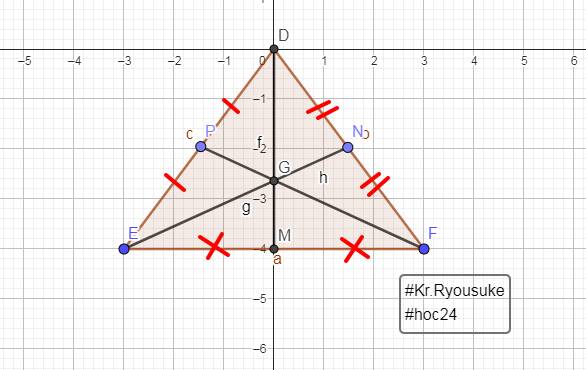
co tam giác DEF có đường trung tuyến DM và EN cắt nhau tại G
Biết DM=9cm, tính DG,GM
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



`\Delta DEF` có:
\(\text{DM}\cap\text{EN}\cap\text{FP}=\text{G}\)
Mà \(\text{DM, EN, FP}\) là các đường trung tuyến
`->`\(\text{G là trọng tâm của }\Delta\text{DEF}\)
A. `GD = 2GM` (đúng)
B. EN = 3GN (đúng)
C. `(GF)/(FP)=1/3` (sai)
`-` Khoảng cách từ trọng tâm đến đỉnh là `2/3` chứ không phải `1/3`.
D. `(EG)/(EN) = 2/3` (đúng)
Xét các đáp án trên `-> C (tm).`

có ΔEDF cân ở D =>DE=DF; góc E =góc F
xét ΔDEM và ΔDFM có
DM là trung tuyến => EM=FM
góc E =góc F (cmt)
DE=DF (cmt)
=>ΔDEM = ΔDFM (cgc)
b)Có Δ DEF cân mà DM là trung tuyến
=> DM là đường cao (tc Δ cân )
=> DM⊥EF
c) EM=FM=EF/2=5
xét ΔDEM có DM ⊥ EF => góc EMD =90o
=>EM2+DM2=ED2 (đl pitago)
=>52+DM2=132 => DM=12
d) Ta có G là trọng tâm của ΔDEF
=>DG=2/3DM=> DG=2/3*12=8


a) Ta có .
Ta lại có là giao điểm của và là trọng tâm của tam giác
.
Suy ra .
Chứng minh tương tự ta được .
b) Xét tam giác và tam giác có (chứng minh trên);
(hai góc đối đỉnh);
(chứng minh trên).
Do đó (c.g.c)
(hai cạnh tương ứng).
Theo chứng minh trên (hai góc tương ứng).
Mà và ờ vị trí so le trong nên // .
a) Ta có .
Ta lại có là giao điểm của và là trọng tâm của tam giác
.
Suy ra .
Chứng minh tương tự ta được .
b) Xét tam giác và tam giác có (chứng minh trên);
(hai góc đối đỉnh);
(chứng minh trên).
Do đó (c.g.c)
(hai cạnh tương ứng).
Theo chứng minh trên (hai góc tương ứng).
Mà và ờ vị trí so le trong nên // .
Xét \(\Delta DEF\)
DM, EN là các đường trung tuyến (gt)
\(DM\cap EN=\left\{G\right\}\)
=> G là trọng tâm của \(\Delta DEF\) (tính chất 3 đường trung tuyến)
=> DG = \(\frac{2}{3}DM\) (tính chất trung tuyến)
=> DG = \(\frac{2}{3}.9\) (thay số)
=> DG = 6 (cm)
DG + GM = DM (tính chất cộng đoạn thẳng)
6 + GM = 9 (thay số)
GM = 3 (cm)