tìm x,y thỏa mãn x2-2y=y2-2x=3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
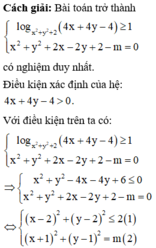


log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B





ta có: x^2-2y=y^2-2x
<=> x^2-2y-y^2+2x=0
<=> (x^2-y^2) + 2x-2y=0
<=> (x-y)(x+y)+2*(x-y)=0
<=> (x-y)(x+y+2)=0
=> x-y=0 và x+y+2=0
=> x-y=0 và x+y=-2
=> x-y-x-y=0+2 (trừ vế với vế)
<=> -2y=2
=> y=-1
=> x=-1
vậy x=y=-1 thf thỏa mãn đề bài