Cho hai đường tròn (O) và (O’) cắt nhau tại A và B (O và O’ nằm về hai phía của AB). Một cát tuyến qua A cắt (O) ở P và cắt (O’) ở Q (P, Q khác A và nằm về hai phía đối với A). 1/ Vẽ OH và O’H’ vuông góc với PQ, chứng minh PQ = 2 HH’. 2/ Chứng minh tam giác PBQ đồng dạng tam giác OAO’. 3/ Xác định vị trí của PQ để PA = QA.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
5 tháng 2 2022
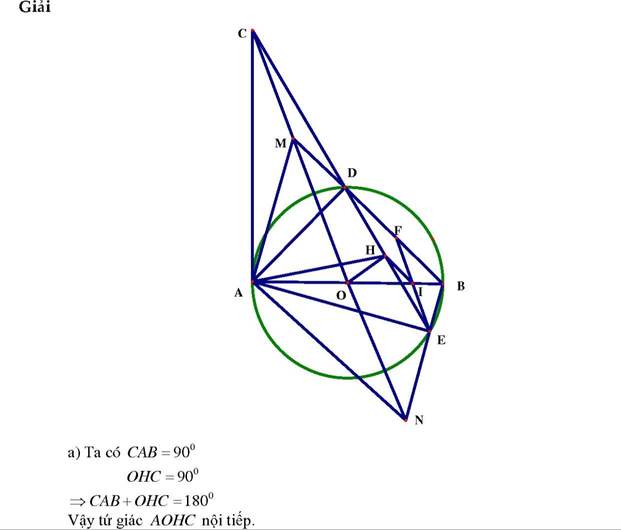
Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F.
Suy ra: Góc HEI = góc HCO
Vì tứ giác AOHC nội tiếp nên:
Góc HAO= góc HEI= góc HCO
<=> Tứ giác AHIE nội tiếp suy ra: góc IHE= góc IAE= góc BDE
=> HI//BD
Mà H là trung điểm của DE
=> I là trung điểm của EF.
Ta có: EF//MN và IE=IF
=> O là trung điểm của đoạn thẳng MN (1)
Từ (1) suy ra:
Tứ giác AMBN là hình bình hành => AM//BN(₫pcm)
17 tháng 5 2021
a) Xét (O) có
\(\widehat{EFA}\) là góc nội tiếp chắn cung EA
\(\widehat{EBA}\) là góc nội tiếp chắn cung EA
Do đó: \(\widehat{EFA}=\widehat{EBA}\)(Hệ quả góc nội tiếp)
hay \(\widehat{MBE}=\widehat{MFA}\)
Xét ΔMBE và ΔMFA có
\(\widehat{MBE}=\widehat{MFA}\)(cmt)
\(\widehat{AMF}\) chung
Do đó: ΔMBE∼ΔMFA(g-g)
Suy ra: \(\dfrac{MB}{MF}=\dfrac{ME}{MA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=ME\cdot MF\)(Đpcm)
HH
16 tháng 11 2020
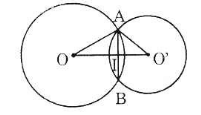
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có
\(AB\perp OO'\) ; AI = IB = 12
Áp dụng định lí Pitago , ta được :
\(OI=\sqrt{OA^2-AI^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\left(cm\right)\)
\(IO'=\sqrt{O'A^2-AI^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\left(cm\right)\)
Vậy OO' = OI + IO' = 16 + 9 = 25 ( cm )
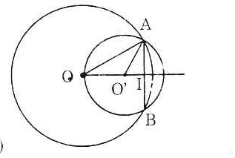
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Như TH1 , ta lại có :
\(OI=\sqrt{OA^2-AI^2}=16\left(cm\right)\)
\(O'I=\sqrt{O'A^2-AI^2}=9\left(cm\right)\)
Vậy OO' = OI – O'I = 16 – 9 = 7 ( cm )