Giúp em bài này với ạ. Em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)

1. What size shoes do you take?
2. What newspaper do you read?
3. What color are your eyes?
4. What time did you arrive this morning?
5. What kind of film do you like?
6. How tall is your teacher?
7. How far is it from your house to the office?
8. How much did you pay for your new shirt?
9. How often do you take an English test in class?
10. How long have you been studying English?

a/ Vì tb đang xếp thành 1 hàng => tb đang ở kì giữa NP hoặc GP2
Nếu ở Kì giữa NP => 2n = 24
Nếu ở KÌ giữa GP 2 => 2n = 48
b/ Vì các NST kép đang phân li về 2 cực => Tb đang ở kì sau GP1 => 2n = 32

câu 3.
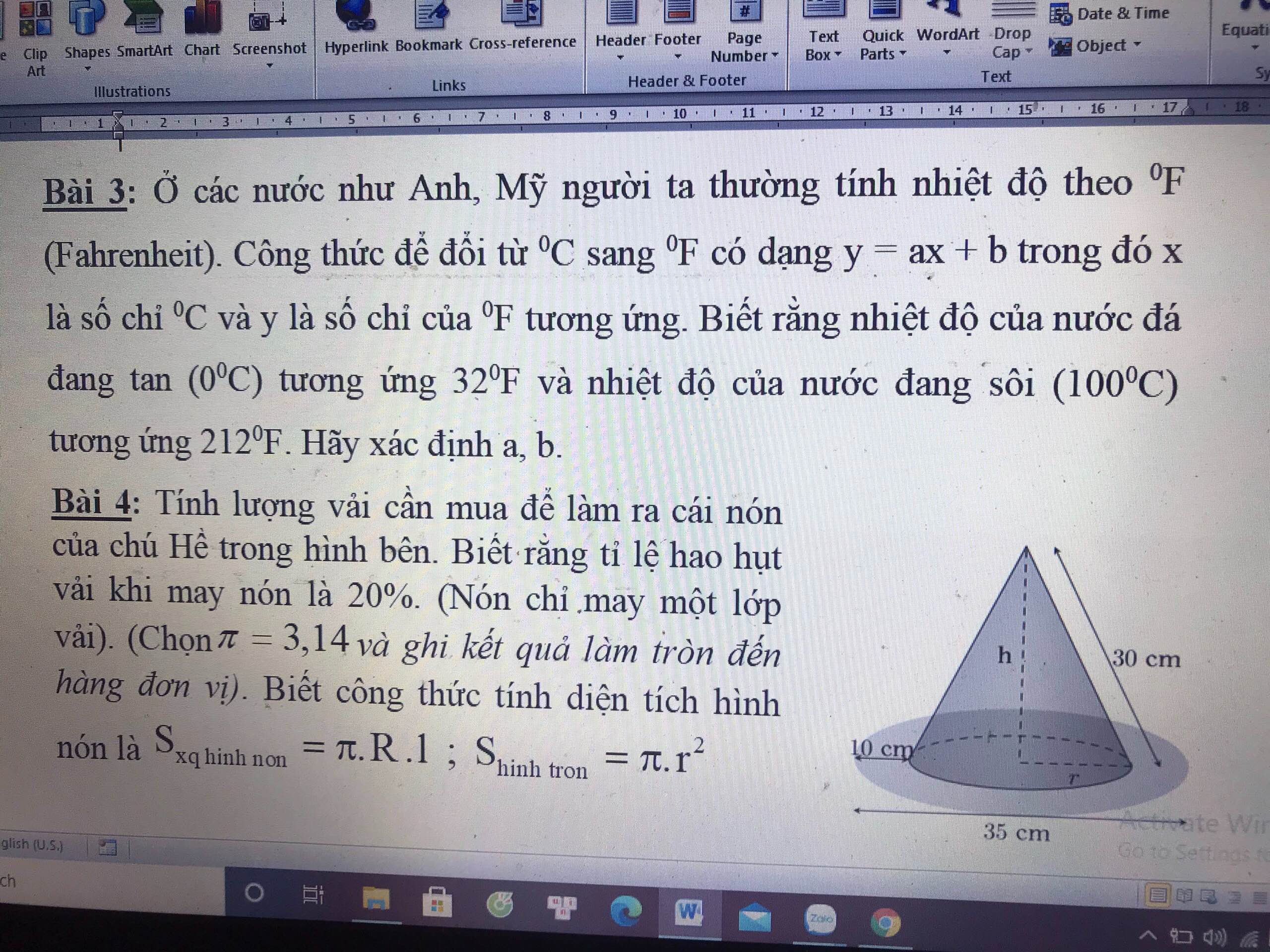
Ta biết rằng khi chuyển đổi từ \(^oC->^oF\) ta có công thức
\(y=ax+b\)(trong đó x là số chỉ \(^oC\), y là chỉ \(^oF\))
theo bài ra=>hệ pt:\(\left\{{}\begin{matrix}32=a.0+b\\212=100a+b\end{matrix}\right.< =>\left\{{}\begin{matrix}b=32\\a=1,8\end{matrix}\right.\)
câu 4:
đường kính nón : \(35-10-10=15cm\)
=>bán kính nón: \(R=\dfrac{15}{2}=7,5cm^{ }\)
=>Sxq(nón)=\(\pi Rl=3,14.30.7,5\approx707cm^2\)
S(vành nón)=\(\pi\left(\dfrac{35}{2}\right)^2-\pi.\left(\dfrac{15}{2}\right)^2=785cm^2\)
S(vải cần thiết)=\(707+785=1492cm^2\)
do hao hụt 20% vải nên số vải cần để khâu mũ là:
\(1492+20\%.1492\approx1790cm^2\)



\(L=\lim\limits_{x\rightarrow+\infty}\left(2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\right)\)
Đặt \(f\left(x\right)=2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\)
Ta có:
\(2.f\left(x\right)=4x^2-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(4x^2-1\right)-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)+\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
Đặt \(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(=\dfrac{\left(2x-1\right)\left(8x^3+12x^2+6x+1-8x^3-12x^2+3x\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(=\dfrac{\left(2x-1\right)\left(9x+1\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}A\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2-\dfrac{1}{x}\right)\left(9+\dfrac{1}{x}\right)}{\left(2+\dfrac{1}{x}\right)^2+\sqrt[3]{\left(8+\dfrac{12}{x}-\dfrac{3}{x^2}\right)^2}+\left(2+\dfrac{1}{x}\right)\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}\)
\(=\dfrac{2.9}{2^2+4+2.2}\)
\(=\dfrac{3}{2}\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(=\dfrac{\left(4x^2-4x+1-4x^2+4x\right).\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(=\dfrac{\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}B\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}{2-\dfrac{1}{x}+\sqrt{4-\dfrac{4}{x}}}\)
\(=\dfrac{2}{2+2}\)
\(=\dfrac{1}{2}\)
\(\Rightarrow2L=\lim\limits_{x\rightarrow+\infty}\left[2f\left(x\right)\right]\)
\(=\lim\limits_{x\rightarrow+\infty}\left[1+A\left(x\right)+B\left(x\right)\right]\)
\(=1+\lim\limits_{x\rightarrow+\infty}A\left(x\right)+\lim\limits_{x\rightarrow+\infty}B\left(x\right)\)
\(=1+\dfrac{3}{2}+\dfrac{1}{2}\)
\(=3\)
\(\Rightarrow L=\dfrac{3}{2}\)
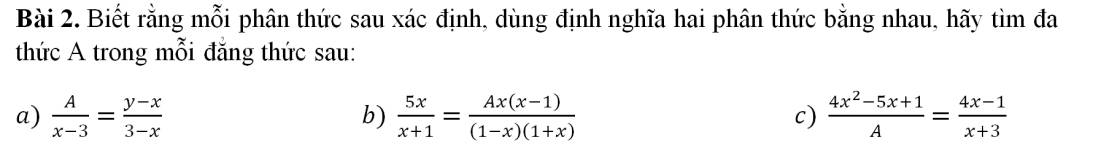 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 



 giúp em bài này với ạ. Em cảm ơn
giúp em bài này với ạ. Em cảm ơn
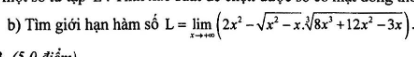
a) xét tg ABD và tg ACD có :
AB = AC (gt)
AD chung
Góc BAC = góc DAC( AD là p/g góc BAC)
=> tg ABD = tg ADC( c-g-c)
b)xét tg AMB và tg AMC có:
AM chung
AB = AC (gt)
góc BAM = góc CAM ( M thuộc AD)
=> tg ABM = tg ACM ( c-g-c)
c)vì tg ADB = tg ADC (cmt)
=> DB = DC (cạnh tương ứng )
Vì tg AMB = tg AMC (cmt)
=> BM = MC (cạnh tương ứng)
Xét tg MBD và tg MCD có
MB= MC (cmt)
MD chung
BD = DC ( cmt)
=> tg MBD = tg MCD ( c-c-c)