EM CẦN GẤP Ạ..
Cho đường tròn tâm O có bán kính OA=R,vẽ dây AB sao cho AB=R.K đối xứng với O qua A.
a)KB là tiếp tuyén của (O).
b)Tính KB theo R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 10 2021
a: Xét ΔBKO có
BA là đường trung tuyến ứng với cạnh OK
\(BA=\dfrac{1}{2}KO\)
Do đó: ΔBKO vuông tại B
hay BK là tiếp tuyến của (O)
b: \(KB=\sqrt{4R^2-R^2}=R\sqrt{3}\)
AT
2 tháng 7 2021
Vì AB là dây đi qua tâm O \(\Rightarrow AB\) là đường kính của \(\left(O,R\right)\)
\(\Rightarrow\angle ACB=90\Rightarrow\Delta ABC\) vuông tại C
b) CD cắt AB tại E
Vì C và D đối xứng với nhau qua AB \(\Rightarrow\angle ACD=\angle ADC\)
mà \(\angle ACD=\angle ACE=90-\angle CAB=\angle CBA\)
\(\Rightarrow ACBD\) nội tiếp \(\Rightarrow D\in\left(O,R\right)\)
AH
Akai Haruma
Giáo viên
30 tháng 9 2021
Lời giải:
a.
$OB=OC$ nên tam giác $OBC$ cân
Do đó đường cao $OH$ đồng thời là trung tuyến hay $H$ là trung điểm $BC$
$\Rightarrow BH=4$ (cm)
Do $BA$ là tiếp tuyến $(O)\Rightarrow BA\perp BO$
Áp dụng HTL trong tam giác vuông với tam giác $ABO$:
$\frac{1}{AB^2}+\frac{1}{BO^2}=\frac{1}{BH^2}$
$\frac{1}{AB^2}+\frac{1}{5^2}=\frac{1}{4^2}$
$\Rightarrow AB=\frac{20}{3}$ (cm)
$AO=\sqrt{AB^2+BO^2}=\sqrt{(\frac{20}{3})^2+5^2}=\frac{25}{3}$ (cm)
b.
Vì $AO$ cắt $BC$ tại trung điểm $H$ của $BC$ và $AO\perp BC$ nên $AO$ là đường trung trực của $BC$
$\Rightarrow AC=AB$. Mà $OB=OC$ nên:
Do đó $\triangle ACO=\triangle ABO$ (c.c.c)
$\Rightarrow \widehat{ACO}=\widehat{ABO}=90^0$
$\Rightarrow AC\perp CO$ nên $AC$ là tiếp tuyến $(O)$
$AC=AB=\frac{20}{3}$ (cm)
28 tháng 8 2023
a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)
CM
9 tháng 4 2017
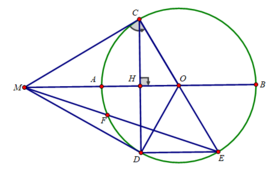
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
CH.OM = CM.CO
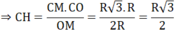
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
7 tháng 11 2016
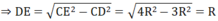
Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được
\(a,AB=OA=OK=R=\dfrac{1}{2}OK\) nên tg OBK vuông tại B nên \(BK\perp OB\)
Do đó BK là tt của B với (O)
\(b,\) Áp dụng PTG cho tg OBK vg tại B
\(KB=\sqrt{OK^2-OB^2}=\sqrt{4R^2-R^2}=\sqrt{3R^2}=R\sqrt{3}\left(đv\right)\)