Cho (E) \(\frac{x^2}{169}+\frac{y^2}{25}=1\)
Diện tích hình vuông có các cạnh đều tiếp xúc với elip là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Từ phương trình chính tắc của (E) ta có: \(a = 7,b = 5 \Rightarrow c = 2\sqrt 6 {\rm{ }}(do{\rm{ }}{{\rm{c}}^2} + {b^2} = {a^2})\)
Vậy ta có tọa độ các giao điểm của (E) với trục Ox, Oy là: \({A_1}\left( { - 7;{\rm{ }}0} \right)\)\({A_2}\left( {7;{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ 5}}} \right)\)\({B_2}\left( {0;{\rm{ 5}}} \right)\)
Hai tiêu điểm của (E) có tọa độ là: \({F_1}\left( { - 2\sqrt 6 ;0} \right),{F_2}\left( {2\sqrt 6 ;0} \right)\)
KK
8 tháng 2 2017
\(C1:\)\(S\)\(=225\)\(cm^2\)\(\Leftrightarrow\)\(S=\left(4x-1\right)^2\)
\(\Rightarrow\left(4x-1\right)^2=225\)
\(\Rightarrow\left(4x-1\right)^2=15^2\Rightarrow4x-1=15\)
\(\Rightarrow4x=16\)
\(\Rightarrow x=4\)
CM
16 tháng 3 2017
Chọn A.
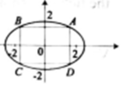
Giả sử ABCD là hình vuông nội tiếp elip
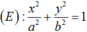
Khi đó các đỉnh A, B, C, D phải nằm trên một trong hai đường phân giác của góc phần tư thứ nhất và thứ 2. Giả sử A(m, m) với m > 0 . Khi đó A B = 2 m và
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
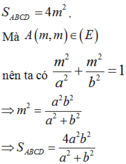
Phương trình chính tắc của elip là: c) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\).
a) Không là PTCT vì a =b =8
b) Không là PTCT
d) Không là PTCT vì a =5 < b =8.
KC
5 tháng 8 2017
Hahaha. Hỏi một phát 5 câu lun hả bà!!!!!
Bài 5 nhé:
Ta có: (làm hơi tắt nhưng cái này cậu tự biến đổi đc)
\(y=72x-\sqrt{\frac{5x^5-16277165}{20}}\) => \(5x^5-\frac{16277165}{20}\ge0\)( vì có căn nên cái bên trong lun lớn hon hoặc = 0)
=> \(x\ge\sqrt[5]{\frac{16277165}{5}}=20,0688....\)mà x nguyên dương => \(x\ge21\)
Nhập vào máy tính: X = X+1 : 72X - \(\sqrt{\frac{5x^5-16277165}{20}}\)
Sau đó ấn CALC 20 = = = .... ( ấn liên tiếp phím = tìm các giá trị \(72x-\sqrt{\frac{5x^5-16277165}{20}}\)nguyên dương, đến khi \(72x-\sqrt{\frac{5x^5-16277165}{20}}\)âm thì dừng)
=> Các cặp số (x;y) thỏa mãn đề bài là (29;11)