Cho (P) : y=x²+2 và đường thẳng d: mx+3 với m thuộc R. Giả sử đường d cắt (P) tại hai điểm A và B. Gọi S là diện tích hình phẳng được giới hạn bởi đường thẳng d và (P). Khi S nhỏ nhất thì giá trị biểu thức P=(xA.yA)²+(xB.yB) ² bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 11 2019
Chọn đáp án A
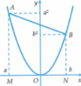
Giả sử A a ; a 2 và B b ; b 2 là hai điểm thuộc (P) và thỏa mãn AB = 2018.
Phương trình đường thẳng d đi qua hai điểm A và B là
Diện tích hình phẳng giới hạn bởi (P) và đường thẳng d là:
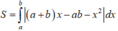
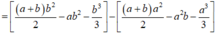
= 1 6 b - a 3
Gọi M là hình chiếu của A trên Ox và N là hình chiếu của B trên Ox. Suy ra M(a;0) và N(b;0).
Ta luôn có M N ≤ A B hay b - a = b - a ≤ 2018 .
Dấu “=” xảy ra khi MN//AB hay AB//Ox. Khi đó a = -1009; b = 1009.
Vậy S = 1 6 b - a 3 = 2018 3 6
CM
23 tháng 5 2019
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số
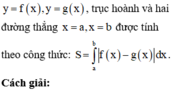
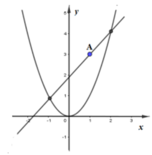
Diện tích hình phẳng giới hạn bởi parabol (P) và đường thẳng d:
S = ∫ x 1 x 2 k x − k + 3 − x 2 d x = 1 2 k x 2 − k − 3 x − 1 3 x 3 x 2 x 1 = 1 2 k x 1 2 − k − 3 x 1 − 1 3 x 1 3 − 1 2 k x 2 2 − k − 3 x 2 − 1 3 x 2 3 = 1 2 k x 1 2 − x 2 2 − k − 3 x 1 − x 2 − 1 3 x 1 3 − x 2 3 = x 1 − x 2 1 2 k x 1 + x 2 − k − 3 − 1 3 x 1 + x 2 2 − x 1 x 2 = x 1 − x 2 1 2 k . k − k − 3 − 1 3 k 2 − k − 3 = x 1 − x 2 1 6 k 2 − 2 3 k + 2
CM
25 tháng 2 2019
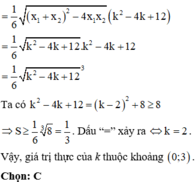
Phương trình hoành độ giao điểm của (P) và d là x 2 - m x - 1 = 0
Ta có ∆ = m 2 + 4 > 0 ∀ m . Suy ra phương trình luôn có 2 nghiệm phân biệt x 1 ; x 2
Giả sử x 1 < x 2 . Khi đó:
S = ∫ x 1 x 2 m x + 2 - x 2 - 1 d x = ∫ x 1 x 2 m x + 1 - x 2 d x = m 2 + 4 m 2 6 + 2 3 ≥ 4 3
Vậy m i n S = 4 3 ⇔ m = 0
Đáp án D
CM
8 tháng 7 2018
Chọn đáp án B
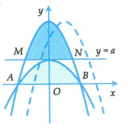
Để việc tính toán trở nên đơn giản, ta tịnh tiến hai parabol sang trái một đơn vị. Khi đó, phương trình các parabol mới là
CM
26 tháng 7 2018
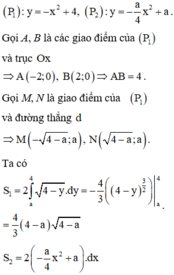
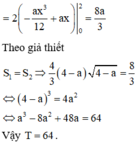
Đáp án A.
= x 2 − x 1 − 1 3 x 1 + x 2 2 − x 1 x 2 + m 2 x 1 + x 2 + 1
CM
25 tháng 7 2019
Có d qua điểm A(1;2) và có hệ số góc k có phương trình là d; y=k(x-1)+2
Phương trình hoành độ giao điểm: 
Khi đó diện tích hình phẳng
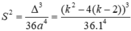
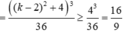
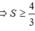
Chọn đáp án C.
*Chú ý diện tích hình phẳng giới hạn bởi parabol
y
=
a
x
2
+
b
x
+
c
và đường thẳng d:y=mx+n có công thức tính nhanh sau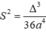 
trong đó Δ là biệt thức của phương trình hoành độ giao điểm:
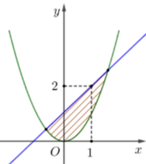
Phương trình hoành độ giao điểm:
\(x^2+2=mx+3\Leftrightarrow x^2-mx-1=0\)
\(ac=-1< 0\Rightarrow\) d luôn cắt (P) tại 2 điểm phân biệt A, B có hoành độ trái dấu, giả sử A là điểm có hoành độ âm
Diện tích hình phẳng:
\(S=\int\limits^{x_B}_{x_A}\left(mx+3-x^2-2\right)dx=\frac{1}{2}mx_B^2+x_B-\frac{1}{3}x_B^3-\frac{1}{2}mx_A^2-x_A+\frac{1}{3}x_A^3\)
\(=\left(x_B-x_A\right)\left(\frac{1}{2}m\left(x_A+x_B\right)+1-\frac{1}{3}\left(\left(x_A+x_B\right)^2-x_Ax_B\right)\right)\)
\(=\left(x_B-x_A\right)\left(\frac{1}{2}m^2+1-\frac{1}{3}\left(m^2+1\right)\right)=\frac{1}{6}\left(m^2+4\right)\left(x_B-x_A\right)\)
\(=\frac{1}{6}\left(m^2+4\right)\sqrt{m^2+4}\ge\frac{4}{3}\)
\(\Rightarrow S_{min}\) khi \(m=0\Rightarrow x^2-1=0\Rightarrow\left\{{}\begin{matrix}x_A=-1\Rightarrow y_A=3\\x_B=1\Rightarrow y_B=3\end{matrix}\right.\)
\(\Rightarrow P=18\)