trong mặt phẳng hệ trục tọa độ OXY ,tính góc lượng giác GIỮA đt √3x -y+1 =0 với trục hoành
A 45* b135* C 60* D120*
...
Đọc tiếp
trong mặt phẳng hệ trục tọa độ OXY ,tính góc lượng giác GIỮA đt √3x -y+1 =0 với trục hoành
A 45* b135* C 60* D120*
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 4 2019
Đường thẳng được viết lại \(y=\sqrt{3}.x-1\)
\(\Rightarrow\)\(tan\alpha=\sqrt{3}\)
\(\Rightarrow\alpha=60^o\)
=> Chọn c
6 tháng 4 2016
Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)
29 tháng 12 2020
Phần b mk chưa học nên chịu :v
a, Phương trình đường thẳng (d) là: y = ax + b
Vì đường thẳng (d) song song với đường thẳng y = 3x + 1 nên
\(\Rightarrow\) \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)
Với a = 3 ta được pt đường thẳng (d): y = 3x + b
Vì đường thẳng (d) đi qua điểm A(3;7) nên thay x = 3; y = 7 ta được:
7 = 3.3 + b
\(\Leftrightarrow\) b = -2 (TM)
Vậy phương trình đường thẳng (d) là: y = 3x - 2
Chúc bn học tốt!
CM
5 tháng 6 2017
a) Đúng. Giả sử A(a; b); O(0; 0)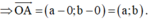 
b) Đúng
c) Đúng
d) Đúng Vì tia phân giác của góc phần tư thứ nhất là đường thẳng y = x.
MN
23 tháng 5 2020
\(\overrightarrow{n_{d1}}=\left(1;2\right)\) ; \(\overrightarrow{n_{d2}}=\left(3;m\right)\)
Ta có: cos(d1;d2) = \(\left|cos(\overrightarrow{n_{d1};}\overrightarrow{n_{d2}})\right|\) = \(\frac{\sqrt{2}}{2}\)
=> \(\frac{3+2m}{\sqrt{\left(3+m^2\right)5}}\) = \(\frac{\sqrt{2}}{2}\) ⇔ 2(3 + 2m) = \(\sqrt{10\left(3+m^2\right)}\)
=> ĐK: 3 + 2m > 0 ⇔ m > \(\frac{-3}{2}\)
trục hoành có phương trình y=0
\(\cos=\frac{1}{\sqrt{3+1}\sqrt{1}}=\frac{1}{2}\)
=> 60o
ta có đt y = -\(\sqrt{3}\)x -1
vì \(-\sqrt{3}< 0\) hàm số của đt nghịch biến trên R
gọi α là góc tạo bởi đt với trục hoành, ta có tanα = -a = \(\sqrt{3}\)(a là hệ số góc)
nên α = 120o