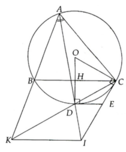
Cho đường tròn ( O ), dây BC cố định. Trên cung lớn BC của ( O , lấy điểm A ( sao cho AB < AC ). Hai tiếp tuyến qua B và C của ( O ) cắt nhau tại E
1) CM tứ giác BOCE nội tiếp
2) AE cắt ( O ) tại điểm thứ 2 là D. CMR : EB^2=ED.EA
3) Gọi F là trung điểm của AD. Đường thẳng qua D và song song với EC cắt BC tại G. CMR GF // AC
Giải câu 3 đầy đủ 3 ticks ..