Cho tam giác ABC nhọn nội tiếp trong đường tròn (O). Gọi D là điểm chính giữa của cung nhỏ AB. Vẽ bán kính OE vuông góc với AC. Dây DE cắt AB, AC lần lượt tại H và K.
a) Chứng minh hai góc AHK và AKH bằng nhau
b) Gọi I là giao điểm của BE và CD. Chứng minh CEKI nội tiếp và IK//AB
c) Gọi F là giao điểm của AB và CD. Chứng minh AI.FC<IC.AF+IF.AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 11 2023
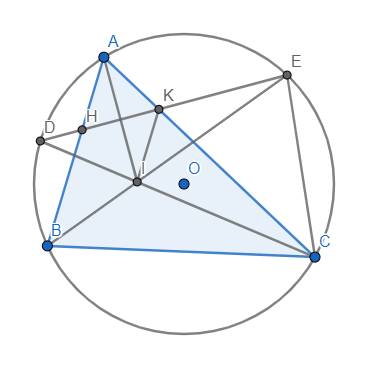
a) Ta có \(\widehat{AHK}=\dfrac{sđ\stackrel\frown{AE}+sđ\stackrel\frown{BD}}{2}\)
và \(\widehat{AKH}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\)
Mặt khác, do D, E lần lượt là điểm chính giữa của cung AB, AC nên \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD};sđ\stackrel\frown{AE}=sđ\stackrel\frown{CE}\). Từ đó \(\Rightarrow\widehat{AHK}=\widehat{AKH}\) hay tam giác AHK cân tại A (đpcm).
b) Hiển nhiên I là tâm đường tròn nội tiếp tam giác ABC \(\Rightarrow\) AI là tia phân giác của \(\widehat{BAC}\) (hay chính là \(\widehat{HAK}\)). Mà theo câu a), tam giác AHK cân tại A nên AI đồng thời là đường cao của tam giác AHK \(\Rightarrow AI\perp HK\) hay \(AI\perp DE\) (đpcm)
c) Ta có \(\widehat{CIE}=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{BD}}{2}\)
\(=\dfrac{sđ\stackrel\frown{CE}+sđ\stackrel\frown{AD}}{2}\) \(=\widehat{CKE}\) nên tứ giác CEKI nội tiếp
\(\Rightarrow\widehat{HKI}=\widehat{DCE}\) \(=\dfrac{sđ\stackrel\frown{DE}}{2}\)
\(=\dfrac{sđ\stackrel\frown{DA}+sđ\stackrel\frown{AE}}{2}\) \(=\dfrac{sđ\stackrel\frown{BD}+sđ\stackrel\frown{AE}}{2}\) \(=\widehat{AHK}\)
Từ đó dễ dàng suy ra KI//AH hay KI//AB (đpcm)
NH
28 tháng 5 2017
1.khỏi cần nói nhiều
2. Ta có TG AHB vuông => AD.AB = AH^2 (1)
TG AHC vuông =>AE.AC = AH^2 (2) Từ 1 và 2 => AD.AB=AE.AC
Cái vẽ đường kính OAK là cái hell gì vậy
GH
18 tháng 3 2021
a)Xét (O) có
ac là dây
e là điểm chính giữa cung ac
=>OE vuông góc AC=> EHC = 90(1)
Có AEB là góc nội tiếp chắn cung AB
=> AEB =90
Mà KC // EB
=>EK vuông góc KC=>EKC=90(2)
Từ (1)(2)=>EKC+EHC=180
Mà 2 góc nằm ở vị trí đối nhau của tứ giác CHEK
=>tứ giác CHEK nội tiếp(đpcm)
b)Gọi giao điểm của KH với AB là I
Có tứ giác CHEK nội tiếp (câu a)
=>EKH=ECH(3)
Có tứ giác AECB nội tiếp
=>ECA=EBA(4)
Từ (3)(4)=>EKH=EBA
Xét 2 tam giác AKI và ABE có
A:chung
AKI=ABE(cmt)
=>AKI\(\sim\)ABE
=>AIK=AEB=90
=>KH\(\perp\)AB(đpcm)