Gọi (c) là đồ thị của hàm số y = x3/3-x2+2x+1 viết phương trình tiếp tuyến của (c) biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại Avà B sao cho tam giác OAB vuông cân (O là gốc toạ độ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Gọi M(a; b) là toạ độ của tiếp điểm
Đạo hàm y ' = - 1 ( 2 x + 3 ) 2 < 0 ; ∀ x .
+ Do tam giác OAB cân tại O nên tiếp tuyến ∆ song song với đường thẳng y= -x (vì tiếp tuyến có hệ số góc âm).
Nghĩa là
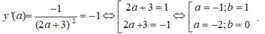
-Với a= -1; b= 1 phương trình ∆: y- 1= -( x+ 1) hay y= -x ( loại) .
-Với a= -2; b= 0 thì ∆ : y- 0= -( x+ 2) hay y=-x-2 (nhận).
Vậy phương trình tiếp tuyến cần tìm là y= -x- 2.
Chọn D.

Đáp án D
Phương pháp:
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x o .
+) Tìm giao điểm của tiếp tuyến với các trục tọa độ.
+) Tính OA, OB, giải phương trình tìm x o → Phương trình tiếp tuyến và kết luận.

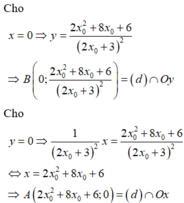
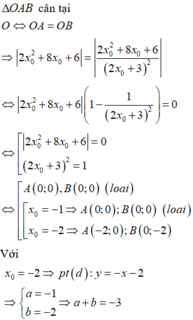

Chọn: D
![]()
![]()
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x 0 là:
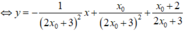
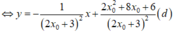
Cho x = 0
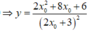
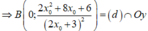
Cho y = 0
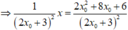
![]()
![]()
∆ O A B c â n t ạ i O ⇔ O A = O B
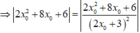
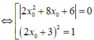
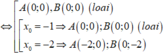
Với x 0 = - 2
![]()
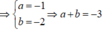


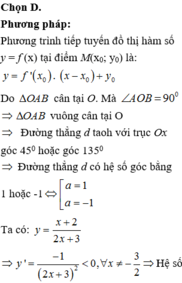
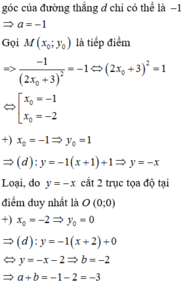


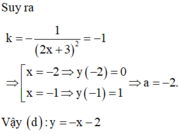




\(y'=x^2-2x+2\)
Gọi tiếp tuyến d tại \(M\left(a;b\right)\) có phương trình:
\(y=\left(a^2-2a+2\right)\left(x-a\right)+\frac{1}{3}a^3-a^2+2a+1\)
Giao của d với Ox và Oy lần lượt là \(\left\{{}\begin{matrix}A\left(\frac{2a^3-3a^2-3}{3\left(a^2-2a+2\right)};0\right)\\B\left(0;\frac{2a^3-3a^2-3}{-3}\right)\end{matrix}\right.\)
\(OA^2=OB^2\Leftrightarrow\frac{\left(2a^3-3a^2-3\right)^2}{9\left(a^2-2a+2\right)^2}=\frac{\left(2a^2-3a^2-3\right)^2}{9}\)
\(\Leftrightarrow\left(a^2-2a+2\right)^2=1\) \(\Leftrightarrow a^2-2a+1=0\Rightarrow a=1\)
Phương trình tiếp tuyến: \(y=x+\frac{4}{3}\)
Giỏi quá mk cảm ơn bạn nhiều