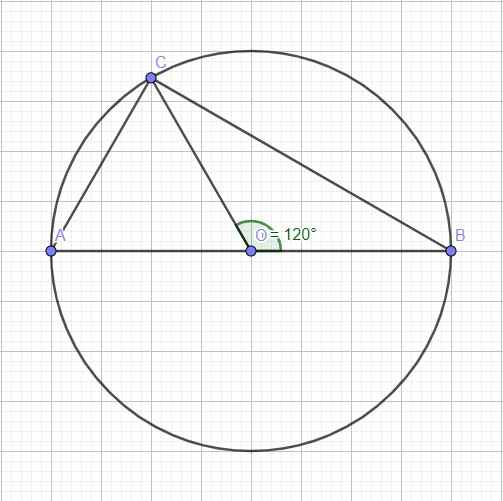
Cho tam giác ABC nội tiếp nửa đường tròn đường kính AB bằng 2r. Nếu góc AOC bằng 120 độ thì độ dài AC bằng bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2021
Do AB là đường kính \(\Rightarrow\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\) Tam giác ABC vuông tại C
Mặt khác \(OA=OC=R\Rightarrow\Delta OAC\) cân tại O (1)
\(\widehat{AOC}=180^0-\widehat{BOC}=60^0\) (2)
(1);(2) \(\Rightarrow\Delta AOC\) đều \(\Rightarrow AC=OA=R\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2-AC^2}=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
10 tháng 10 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2\)=\(AB^2+AC^2\)
⇔\(BC^2\)= 52 + 122 =169
hay BC = 13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay R = \(\dfrac{BC}{2}\)= \(\dfrac{13}{2}\) =6.5(cm)
29 tháng 12 2023
Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2+5^2=10^2\)
=>\(AC^2=75\)
=>\(AC=\sqrt{75}=5\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=5\cdot5\sqrt{3}=25\sqrt{3}\)
=>\(AH=\dfrac{25\sqrt{3}}{10}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
TT
1
KV
22 tháng 12 2023
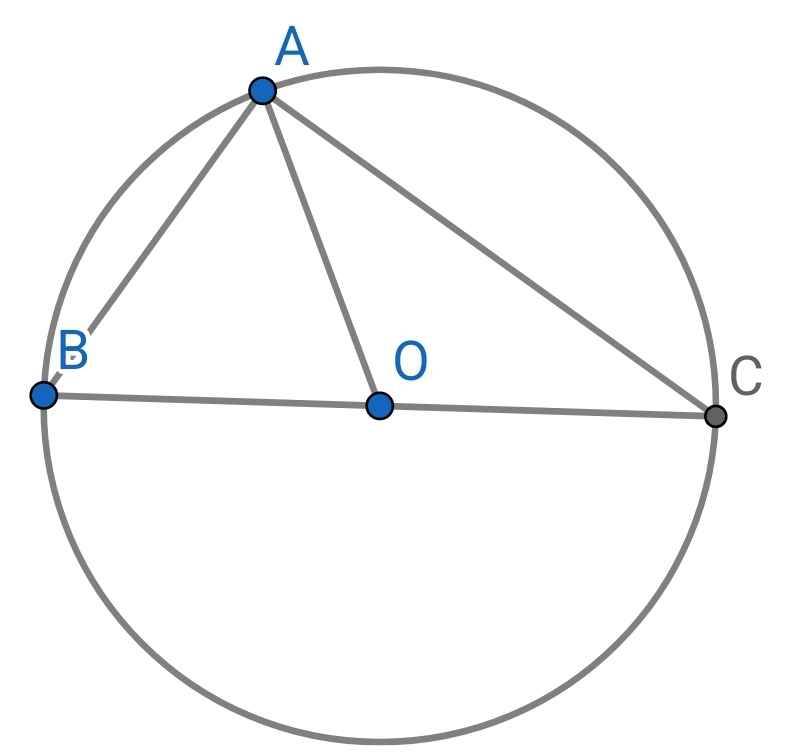Cách 1: Dùng tính chất đường trung tuyến AO bằng nửa cạnh BC
Ta có:
OA = OB = OC = bán kính
⇒ OA = BC : 2
⇒ ∆ABC vuông tại A
⇒ ∠BAC = 90⁰
Cách 2: Dùng định lí
Do ∆ABC nội tiếp (O) đường kính BC
⇒ ∆ABC vuông tại A
⇒ ∠BAC = 90⁰
AH
Akai Haruma
Giáo viên
12 tháng 4 2021
Lời giải:
Ta nhớ lại công thức, trong tam giác $ABC$ có $AB=c, BC=a, CA=b$ thì:
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$.
Ứng vào bài toán, với $\sin A=\sin 120=\frac{\sqrt{3}}{2}$ và $a=BC=6$ thì:
$R=\frac{a}{2\sin A}=\frac{6}{2.\frac{\sqrt{3}}{2}}=2\sqrt{3}$