Cho hàm số f(x)=2mx-mx^3.Số=1là nghiệm của bất phương trình f'(x)≤1khi và chỉ khi
A.m≤-1
B.m≥1
C.-1≤m≤1
D.m≥1
Giải chi tiết hộ mình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
ta có
f ( x ) = 2 m x - m x 3 ⇒ f ' ( x ) = 2 m - 3 m x 2
Vì x= 1 là nghiệm của bất phương trình f ' ( x ) ≤ 1 nên
2 m − 3 m .1 2 ≤ 1 ⇔ − m ≤ 1 ⇔ m ≥ − 1

- Ta có: f ' ( x ) = m - x 2 .
- Do x = -1 là nghiệm của bất phương trình f'(x) < 2.
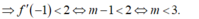
Chọn B.

Ta có f ' x = m − x 2 .
Để x= - 1 là nghiệm của bất phương trình
f ' ( x ) < 2
⇒ f ' 1 < 2 ⇔ m − 1 < 2 ⇔ m < 3.
Chọn đáp án B

Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]

\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m

Đặt ![]() Ta có
Ta có ![]()
Trên đoạn [-2;3] ta có f(x) chỉ đổi dấu khi qua điểm x=1 Do vậy trước tiên cần có x=1 là nghiệm của ![]()
![]()
Điều kiện đủ:
+) Với m=−1
![]()
(đúng)
+) Với m = - 1 3

(đúng).
Vậy m = 1 , m = - 1 3 là các giá trị cần tìm.
Chọn đáp án D.