Cho tam giác ABC. Các phân giác góc B và góc C cắt nhau ở O. Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ O đến BC, CE, AB (D thuộc BC, E thuộc AC, F thuộc AB). Tia AO cắt BC ở M. Chứng minh góc :a)OD=OE=OF b)DOB = góc MOC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

22 tháng 11 2023
a: Xét ΔBDI vuông tại D và ΔBFI vuông tại F có
BI chung
\(\widehat{DBI}=\widehat{FBI}\)
Do đó: ΔBDI=ΔBFI
=>ID=IF
Xét ΔCFI vuông tại F và ΔCEI vuông tại E có
CI chung
\(\widehat{FCI}=\widehat{ECI}\)
Do đó: ΔCFI=ΔCEI
=>IE=IF
b: IE=IF
ID=IF
Do đó: IE=ID
Xét ΔADI vuông tại D và ΔAEI vuông tại E có
AI chung
ID=IE
Do đó: ΔADI=ΔAEI
=>\(\widehat{DAI}=\widehat{EAI}\)
=>\(\widehat{BAI}=\widehat{CAI}\)
=>AI là phân giác của \(\widehat{BAC}\)

CM
16 tháng 7 2019
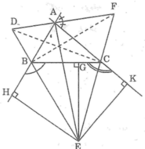
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
\(\Delta\)COE=\(\Delta\)COD(ch-gn)=>OE=OD
\(\Delta\)BOF=\(\Delta\)BOD(ch-gn)=>OD=OF
Suy ra: OD=OE=OF
b) mình nghĩ là ko bằng