Cho n \(\in\)N chứng tỏ: \(A=\dfrac {14n+3}{21n+5}\) là phân số tối giản
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

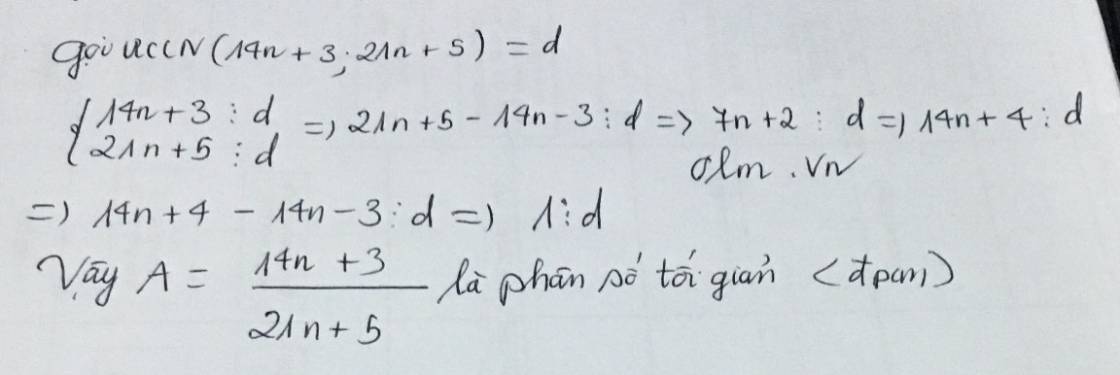

Giả sử UCLN(14n+3;21n+5)=d
14n+3 chia hết cho d nên 42n+9 chia hết cho d
21n+5 chia hết cho d nên 42n+10 chia hết cho d
vay 1 chia hết cho d, d=1
Vậy phân số tối giản
Giải:
Gọi ƯC(14n+3;21n+5)=d
⇒14n+3 ⋮ d ⇒3.(14n+3) ⋮ d ⇒42n+9 ⋮ d
21n+5 ⋮ d 2.(21n+5) ⋮ d 42n+10 ⋮ d
⇒(42n+10)-(42n+9) ⋮ d
⇒ 1 ⋮ d
⇒d=1
Vậy 14n+3/21n+5 là phân số tối giản.
Chúc bạn học tốt!

Gọi d=ƯCLN(14n+3;21n+5)
=>42n+9-42n-10 chia hết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG

Đặt \(\left(14n+3,21n+5\right)=d\).
Suy ra
\(\hept{\begin{cases}14n+3⋮d\\21n+5⋮d\end{cases}}\Rightarrow2\left(21n+5\right)-3\left(14n+3\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.

Gọi d = ƯCLN ( 14n + 3 , 21n + 5 )
Xét hiệu :
\(\left(21n+5\right)-\left(14n+3\right)⋮d\)
\(2\left(21n+5\right)-3\left(14+3\right)⋮d\)
\(42n+10-42n-9⋮d\)
\(10-9⋮d\)
\(1⋮d\)
\(\Rightarrow d\inƯ\left(1\right)\)
\(\RightarrowƯ\left(1\right)=1\Rightarrow d=1\)
Vậy....
#Louis

Gọi \(d\inƯC\left(14n+3,21n+5\right)\)
\(\Rightarrow\hept{\begin{cases}\left(14n+3\right)⋮d\\\left(21n+5\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}3\left(14n+3\right)⋮d\\2\left(21n+5\right)⋮d\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\left(42n+9\right)⋮d\\\left(42n+10\right)⋮d\end{cases}}\)
\(\Rightarrow\left(42n+10\right)-\left(42+9\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d\in\left\{1\right\}\)
\(\Rightarrow1\inƯC\left(14n+3,21n+5\right)\)
\(\Rightarrow\frac{14n+3}{21n+5}\)là phân số tối giản

Gọi \(d=ƯC\left(14n+17;21n+25\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}14n+17⋮d\\21n+25⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}42n+51⋮d\\42n+50⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
\(\Leftrightarrow d\inƯ\left(1\right)\)
\(\Leftrightarrow d\in\left\{1;-1\right\}\)
\(\LeftrightarrowƯCLN\left(14n+17;21n+25\right)=1\)
hay phân số \(B=\dfrac{14n+17}{21n+25}\) là phân số tối giản(Đpcm)

Gọi ƯCLN (14n + 3 ; 21n + 5) = d
=> 14n + 3 chia hết cho d => 3(14n + 3) chia hết cho d
21n + 5 chia hết cho d => 2(21n + 5) chia hết cho d
=>2(21n + 5) - 3(14n + 3) chia hết cho d
=> (42n + 10) - (42n + 9) chia hết cho d
=> d = ±1
=> \(\frac{14n+3}{21n+5}\) là phân số tối giản
Các bạn xem mình làm có đúng không ??
Đặt d = ƯCLN ( 14n + 3,21n + 5 ) ( d ∈ ℕ* )
Ta có : 14 n + 3 ⋮ d và 21n + 5 ⋮ d
⇒ 3( 14n + 3 ) ⋮ và 2( 21n + 5 ) ⋮ d ⇒ 42n + 9 ⋮ d và 42n + 10 ⋮ d
⇒ (42n + 10) - (42n + 9) ⋮ d ⇒ 1 ⋮ d . Do đó : d = 1
Vậy phân số trên là phân số tối giản