tìm m để F min biết F= (2x+y+1)2 + (4x+my+5)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
28 tháng 1 2020
a) \(F\left(x\right)=\left(2x^2-4x+5\right)-\left(x^2-6\right)+2x-3\)
\(=2x^2-4x+5-x^2+6+2x-3\)
\(=\left(2x^2-x^2\right)+\left(2x-4x\right)+\left(5+6-3\right)\)
\(=x^2-2x+8\)
Hệ số tự do của đa thức F(x) là: 8
Hệ số bậc 1 của đa thức F(x) là: -2
b) \(F\left(x\right)=x^2-2x+8\); \(G\left(x\right)=-x^2-2x-9\)
+) \(\Rightarrow F\left(x\right)+G\left(x\right)=\left(x^2-2x+8\right)+\left(-x^2-2x-9\right)\)
\(=\left(x^2-x^2\right)+\left(-2x-2x\right)+\left(8-9\right)=-4x-1\)
Vậy \(M\left(x\right)=-4x-1\)
+) và \(F\left(x\right)-G\left(x\right)=\left(x^2-2x+8\right)-\left(-x^2-2x-9\right)\)
\(=\left(x^2+x^2\right)+\left(-2x+2x\right)+\left(8+9\right)=2x^2+17\)
Vậy \(N\left(x\right)=2x^2+17\)
c)
+) M(x) có nghiệm khị và chỉ khi M(x) = 0
\(\Leftrightarrow-4x-1=0\Leftrightarrow-4x=1\Leftrightarrow x=\frac{-1}{4}\)
Vậy M(x) có 1 nghiệm là \(\frac{-1}{4}\)
+) N(x) có nghiệm khị và chỉ khi N(x) = 0
\(\Leftrightarrow2x^2+17=0\)
Mà \(2x^2+17\ge17\left(dox^2\ge0\right)\)
Nên N(x) vô nghiệm
d) F(x) = x2 - 3\(\Leftrightarrow x^2-2x+8=x^2-3\Leftrightarrow-2x=-11\)
\(\Leftrightarrow x=\frac{11}{2}\)
Vậy \(x=\frac{11}{2}\)thì F(x) = x2 - 3
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Tìm min:
$F=3x^2+x-2=3(x^2+\frac{x}{3})-2$
$=3[x^2+\frac{x}{3}+(\frac{1}{6})^2]-\frac{25}{12}$
$=3(x+\frac{1}{6})^2-\frac{25}{12}\geq \frac{-25}{12}$
Vậy $F_{\min}=\frac{-25}{12}$. Giá trị này đạt tại $x+\frac{1}{6}=0$
$\Leftrightarrow x=\frac{-1}{6}$
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Tìm min
$G=4x^2+2x-1=(2x)^2+2.2x.\frac{1}{2}+(\frac{1}{2})^2-\frac{5}{4}$
$=(2x+\frac{1}{2})^2-\frac{5}{4}\geq 0-\frac{5}{4}=\frac{-5}{4}$ (do $(2x+\frac{1}{2})^2\geq 0$ với mọi $x$)
Vậy $G_{\min}=\frac{-5}{4}$. Giá trị này đạt tại $2x+\frac{1}{2}=0$
$\Leftrightarrow x=\frac{-1}{4}$
23 tháng 12 2023
Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
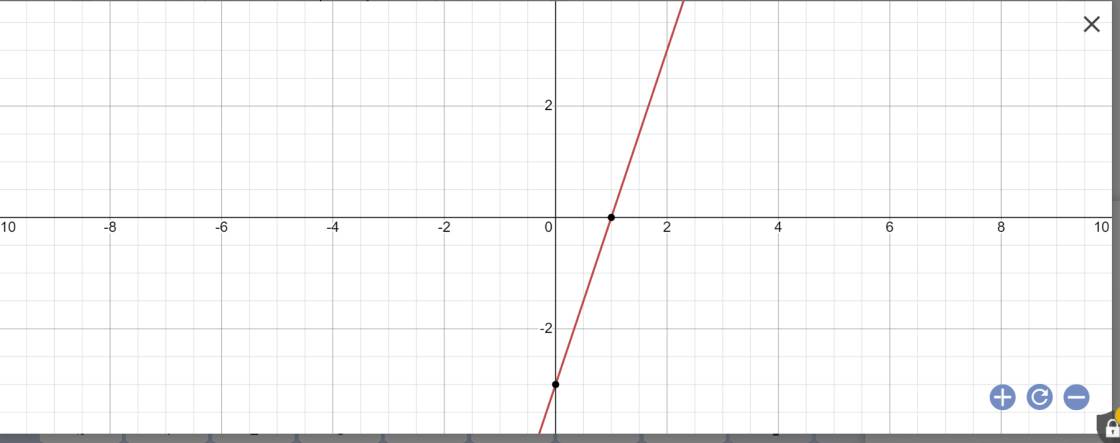
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2
CM
9 tháng 6 2019
Chọn A
Hàm số y = f(x) = 2 x + m x - 1 . xác định và liên tục trên [2;3].
Với m = -2, hàm số trở thành y = 2
(không thỏa)
Với 
ta có: 
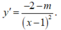
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra 
Do đó: 
Theo giả thiết 
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức 
là không cần thiết.
CM
9 tháng 12 2019
Chọn A
Hàm số y = f(x) =
2
x
+
m
x
-
1
xác định và liên tục trên [2;3]
Với m = -2, hàm số trở thành y = 2 
(không thỏa).
Với m
≠
2, ta có: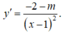 
Khi đó hàm số luôn đồng biến hoặc nghịch biến trên [2;3]
Suy ra
Do đó:
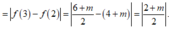
Theo giả thiết
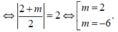
Vậy tổng các giá trị của tham số thỏa mãn yêu cầu bài toán là: -4.
Nhận xét: đề bài cho thêm dấu giá trị tuyệt đối ở trong biểu thức 
là không cần thiết.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
B = 2\(x^2\) - 4\(x\) - 8
B = 2(\(x^2\) - 2\(x\) + 4) - 16
B = 2(\(x-2\))2 - 16
Vì (\(x-2\))2 ≥ 0 ∀ \(x\) ⇒ 2(\(x-2\))2 ≥ 0 ∀ \(x\)
⇒ 2(\(x-2\))2 - 16 ≥ -16 ∀ \(x\)
Dấu bằng xảy ra khi (\(x-2\))2 = 0 ⇒ \(x-2=0\) ⇒ \(x=2\)
Vậy Bmin = -16 khi \(x=2\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
Tìm min của C biết:
C = \(x^2\) - 2\(xy\) + 2y2 + 2\(x\) - 10y + 17
C = (\(x^2\) - 2\(xy\) + y2) + 2(\(x\) - y) + y2 - 8y + 16 + 1
C = (\(x\) - y)2 + 2(\(x\) - y) + 1 + (y2 - 8y + 16)
C = (\(x-y+1\))2 + (y - 4)2
Vì (\(x\) - y + 1)2 ≥ 0 ∀ \(x;y\); (y - 4)2 ≥ 0 ∀ y
Dấu bằng xảy ra khi: \(\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x-y+1=0\\y=4\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-4+1=0\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=-1+4\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Vậy Cmin = 0 khi (\(x;y\)) = (3; 4)
VK
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
Hàm \(f\left(\left|x\right|\right)\) có 5 điểm cực trị khi \(f\left(x\right)\) có 2 cực trị dương
\(\Rightarrow f'\left(x\right)=3x^2-4x+2-m=0\) có 2 nghiệm dương phân biệt
\(\Rightarrow\left\{{}\begin{matrix}\Delta'=4-3\left(2-m\right)>0\\x_1+x_2=\dfrac{4}{3}>0\\x_1x_2=\dfrac{2-m}{3}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m< 2\end{matrix}\right.\) \(\Rightarrow\dfrac{2}{3}< m< 2\)