Tìm các số nguyên n để phân số n+6/n+1 là số nguyên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
1 tháng 4 2020
a) Để C là phân số thì \(n+6\ne0\)
\(\Rightarrow n\ne-6\)
Vậy \(n\ne-6\)
b) Để C là số nguyên thì \(5n-1⋮n+6\)
\(\Rightarrow5n-30+31⋮n+6\)
\(\Rightarrow5\left(n-6\right)+31⋮n+6\)
Mà \(n+6⋮n+6\)
\(\Rightarrow31⋮n+6\)
\(\Rightarrow n+6\inƯ\left(31\right)=\left\{\pm1;\pm31\right\}\)
... (tự làm)
1 tháng 4 2020
Bài chị Vũ Huyền làm gần đúng câu b, cho Mạnh "mạn phép" được sửa lại:
b) Để biểu thức C là 1 số nguyên thì 5n - 1 \(⋮\)n + 6 (n \(\inℤ\))
=> 5n - 1 \(⋮\)n + 6 (n \(\inℤ\))
=> 5n + 30 - 31 \(⋮\)n + 6
=> 5(n + 6) - 31 \(⋮\)n + 6
Vì 5(n + 6) - 31 \(⋮\)n + 6 và 5(n + 6) \(⋮\)n + 6
Nên 31 \(⋮\)n + 6
Tự lm tiếp :))
NN
22 tháng 1
a, Để \(\dfrac{n+1}{n-2}\) có giá trị là một số nguyên thì n + 1 ⋮ n - 2
=> (n - 2) + 3 ⋮ n - 2
Vì (n - 2) ⋮ n - 2 nên 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ∈ {-3;-1;1;3}
=> n ∈ {-1;1;3;5}
b, Để \(\dfrac{4n+5}{2n-1}\) có giá trị là một số nguyên thì 4n + 5 ⋮ 2n - 1
=> (4n - 2) + 7 ⋮ 2n - 1
=> 2(2n - 1) + 7 ⋮ 2n - 1
Vì 2(2n - 1) ⋮ 2n -1 nên 7 ⋮ 2n - 1
=> 2n - 1 ∈ Ư(7) ∈ {-7;-1;1;7}
=> n ∈ {-3;0;1;4}
2 tháng 3 2020
a) Để n+4/n có giá trị nguyên thì n+4\(⋮\)n
Vì n chia hết cho n nên 4 chia hết cho n
-->n thuộc Ư(4)={1;2;4}
Vậy n thuộc {1;2;4}
c) Để 6/n-1 có giá trị nguyên thì 6 chia hết cho n-1
-->n-1 thuộc Ư(6)={1;2;3;6}
+,n-1=1 \(\Rightarrow\)n=2
+,n-1=2 \(\Rightarrow\)n=3
+,n-1=3 \(\Rightarrow\)n=4
+,n-1=6 \(\Rightarrow\)n=7
Vậy n thuộc {2;3;4;7}
23 tháng 6 2021
Câu 1:
a) \(\dfrac{n-5}{n-3}\)
Để \(\dfrac{n-5}{n-3}\) là số nguyên thì \(n-5⋮n-3\)
\(n-5⋮n-3\)
\(\Rightarrow n-3-2⋮n-3\)
\(\Rightarrow2⋮n-3\)
\(\Rightarrow n-3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng giá trị:
| n-1 | -2 | -1 | 1 | 2 |
| n | -1 | 0 | 2 | 3 |
Vậy \(n\in\left\{-1;0;2;3\right\}\)
b) \(\dfrac{2n+1}{n+1}\)
Để \(\dfrac{2n+1}{n+1}\) là số nguyên thì \(2n+1⋮n+1\)
\(2n+1⋮n+1\)
\(\Rightarrow2n+2-1⋮n+1\)
\(\Rightarrow1⋮n+1\)
\(\Rightarrow n-1\inƯ\left(1\right)=\left\{\pm1\right\}\)
Ta có bảng giá trị:
| n-1 | -1 | 1 |
| n | 0 | 2 |
Vậy \(n\in\left\{0;2\right\}\)
23 tháng 6 2021
Câu 2:
a) \(\dfrac{n+7}{n+6}\)
Gọi \(ƯCLN\left(n+7;n+6\right)=d\)
\(\Rightarrow\left[{}\begin{matrix}n+7⋮d\\n+6⋮d\end{matrix}\right.\)
\(\Rightarrow\left(n+7\right)-\left(n+6\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{n+7}{n+6}\) là p/s tối giản
b) \(\dfrac{3n+2}{n+1}\)
Gọi \(ƯCLN\left(3n+2;n+1\right)=d\)
\(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\n+1⋮d\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\3.\left(n+1\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\3n+3⋮d\end{matrix}\right.\)
\(\Rightarrow\left(3n+3\right)-\left(3n+2\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{3n+2}{n+1}\) là p/s tối giản
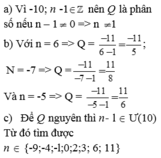
\(\frac{n+6}{n+1}=\frac{n+1+5}{n+1}=1+\frac{5}{n+1}\)
Để ( n + 6 ) \(⋮\)( n + 1 ) thì 5 \(⋮\)( n + 1 ) hay ( n + 1 ) là Ư(5)={ 1 ; -1 ; 5 ; -5 }
Do đó :
- n + 1 = 1 => n = 0
- n + 1 = -1 => n = -2
- n + 1 = 5 => n = 4
- n + 1 = -5 => n = -6
Vậy x \(\in\){ 0; -2; 4; -6 }
Để \(\frac{n+6}{n+1}\)nguyên
=> 1+\(\frac{5}{n+1}\)nguyên
->\(\frac{5}{n+1}\)nguyên
=> n+1 \(\in\)Ư(5)=1;-1;5;-5
Vậy để \(\frac{n+6}{n+1}\)nguyên thì n=0;-2;4;-6