Thầy Dư có 4 đồng xu khác nhau. Trên mỗi mặt của từng đồng xu có ghi đúng một chữ cái. Biết rằng từ những đồng xu này, thầy Dư có thể xếp được các từ sau H O I , T O A N , T I N , T A I , N A N G Hãy xác định các cặp chữ cái viết trên từng đồng xu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải :
Thầy Dư có 4 đồng xu khác nhau, mỗi đồng xu có 2 mặt, mỗi mặt ghi đúng một chữ cái.
=> 4 đồng xu xuất hiện 8 chữ cái.
Mặt khác các từ trên xuất hiện có 7 chữ cái khác nhau nên có một chữ được xuất hiện 2 lần trên các đồng xu.
Xét từ NANG ta thấy trên cùng một từ chữ N được xuất hiện 2 lần trên 2 đồng xu khác nhau.
Như vậy chữ N có thể ghép cặp với bất cứ chữ nào.
Dựa vào các từ trên ta có thể sắp xếp được các chữ có thể ghép cặp với nhau :
+ Chữ H có thể ghép cặp với A, T, N, G
+ Chữ O có thể ghép cặp với G, N
+ Chữ I có thể ghép cặp được với G, N
+ Chữ T có thể ghép cặp với H, G, N
+ Chữ A có thể ghép cặp với H, N
+ Chữ N có thể ghép cặp với H, O, I, G, A, T
+ Chữ G có thể ghép cặp với H, O, I, T
Như vậy có các trường hợp :
+ Trường hợp 1 : O-G , I-N
=> A-H
=> T-N
+ Trường hợp 2 : O-N , I-G
=> A-H
=> T-N
+ Trường hợp 3 : O-N , I-N
=> T-G
=> A-H

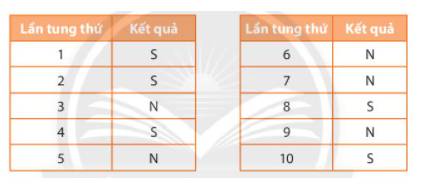
a)
- Bạn Hùng đã tung đồng xu 10 lần. Kết quả của lần thứ nhất là mặt sấp, lần thứ năm là mặt ngửa.
- Có 2 kết quả khác nhau có thể xảy ra, đó là kết quả đồng xu hiện ra mặt sấp hoặc đồng xu hiện ra mặt ngửa.
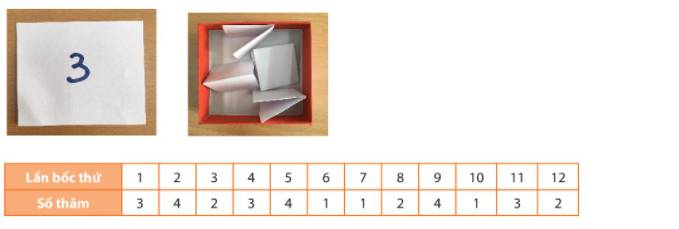
b)
- Kết quả lần thứ 5 là số 4, lần thứ 6 là số 1.
- Có 4 kết quả khác nhau có thể xảy ra, đó là các kết quả 1,2,3,4.

a) Học sinh quan sát đồng xu.
b) Đồng xu có hai mặt: Mặt ngửa và Mặt sấp
Đồng xu có thể xuất hiện mặt ngửa hoặc mặt sấp.

Mình nghĩ lần cân 1 lấy 2 đồng xu ra cân, lần 2 lấy 2 đồng còn lại, nếu khối lượng 2 lần khác nhau thì người đó dùng tiền giả ( trong 2 lần chắc chắn có 1 lần có tiền giả, lần đó cân nặng hơn )
![]()

Câu 1:
Tổng trường hợp: \(N=A_{16}^8\)
- TH1: tặng hết 8 cuốn toán: \(8!\) cách
- TH2: tặng hết 5 cuốn Lý, 3 cuốn còn lại chọn ra từ 11 cuốn \(\Rightarrow C_{11}^3.8!\)
- TH3: tặng hết 3 cuốn Anh, 5 cuốn còn lại chọn ra từ 13 cuốn \(\Rightarrow C_{13}^5.8!\)
Phần bị trùng TH2 và TH3: tặng 5 cuốn Lý và 3 cuốn anh: \(8!\) cách
Tổng cộng: \(n=8!+C_{11}^3.8!+C_{13}^5.8!-8!=\left(C_{11}^3+C_{13}^5\right).8!\)
Xác suất: \(1-\frac{n}{N}=\)
Sao cái đống 8! kia cứ thừa thừa thế nào ấy nhỉ? :D
Câu 2:
Viết lại bài toán: có 8 bạn chưa rõ giới tính xếp vào bàn tròn, tính xác suất để ko có 2 bạn nữ nào ngồi cạnh nhau.
Để ko có 2 bạn nữ ngồi liền kề thì tối đa chỉ có 4 bạn nữ.
- TH1: đúng 1 bạn nữ, luôn đúng, có... cách xếp 1 bạn nữ vào bàn tròn và 7 bạn nam.
- TH2: 2 bạn nữ và 6 bạn nam, xếp 6 bạn nam tạo ra 6 khe trống, xếp 2 bạn nữ này vào 6 khe trống đó
- TH3: 3 bạn nữ, xếp 5 nam tạo 5 khe trống, xếp 3 nữ vào 5 khe trống
- TH4: nam nữ xen kẽ, có đúng 1 cách xếp


Các cặp chữ cái viết trên từng đồng xu là:
N; O
T; G
N; I
H; A
Bạn được vào vòng 2 MYTS rồi à? Chúc mừng nhé! Tôi cũng ôn vào đúng bài này nè.
Chúc Chủ Nhật thi tốt nhé!
Lời giải:
Thầy Dư có 4 đồng xu khác nhau; Mỗi đồng xu có 2 mặt, mỗi mặt có ghi đúng một chữ cái
=>4 đồng xu xuất hiện 8 chữ cái
Mặt khác các từ trên xuất hiện có 7 chữ cái khác nhau nên có một chữ đc xuất hiện 2 lần trên các đồng xu
Xét từ NANG ta thấy trên cùng một từ chữ N đc xuất hiện 2 lần nên chữ N xuất hiện trên 2 đồng xu khác nhau
Như vậy chữ N có thể ghép cặp với bất cứ chữ nào
Dựa vào các từ trên ta có thể sắp xếp đc các chữ có thể ghép cặp với nhau
+) Chữ H có thể ghép cặp với A; T; N; G
+) Chữ O----------------------------G; N
+)Chữ I-------------------------------G, N
+) Chữ T-------------------------------H; G; N
+) Chữ A------------------------------H; N
+)Chữ N------------------------------H; O; I; G; A; T
+) Chữ G---------------------------H; O; I; T
Như vậy có các trường hợp:
TH1: O-G; I-N
=> A-H
=> T-N
TH2: O-N; I-G
=> A-H
=> T-N
Th3: O-N, I-N
=> T-G
=> A-H