Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Tính thể tích và diện tích xung quanh của chóp, biết:
a. Góc trong SB và đáy bằng 45°
b. Góc trong (SCD) và đáy bằng 60°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề bài thiếu 1 dữ liệu nữa (ví dụ SA vuông góc mặt đáy)

Lời giải:
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)

Đáp án D
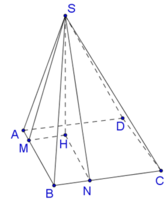
Gọi H là chân đường cao hạ từ S đến mặt phẳng (ABCD). Trong mặt phẳng (ABCD), kẻ HM,HN lần lượt vuông góc với AB,BC.

Vậy thể tích hình chóp S.ABCD là:
![]()

Đáp án D
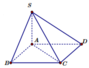
Do đáy hình vuông cạnh a nên đường chéo A C = a 2
S C ; A B C D ⏜ = A C , S C ⏜ = S C A ⏜ = 45 °
⇒ Δ S A C vuông cân tại A ⇒ S A = A C = a 2
V S . A B C D = 1 3 S A B C D . S A = 1 3 a 2 . a 2 = a 3 2 3

Đáp án A
Phương pháp:
Chứng minh góc giữa hai mặt phẳng (SCD) và (ABCD) là SDA bằng cách sử dụng định nghĩa góc giữa hai mặt phẳng là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.
Công thức tính thể tích khối chóp: V = 1 3 S . h
Cách giải:
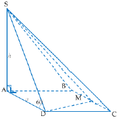
Ta có: S A ⊥ A B C D ⇒ S A ⊥ C D
Mà A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D .
Vì S C D ∩ A B C D = C D A D ⊥ C D S D ⊥ C D nên góc giữa (SCD) và (ABCD) là S D A = 60 °
Ta có: h = a . tan 60 ° = a 3
S A B M D = S A B C D − S Δ D C M = a 2 − 1 2 a . a 2 = 3 a 2 4
⇒ V S . A B M D = 1 3 S A B M D . h = 1 3 . 3 a 2 4 . a 3 = a 3 3 4
Chú ý khi giải:
HS thường xác định sai góc giữa hai mặt phẳng dẫn đến đáp số sai.
a.
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và đáy
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3}{3}\)
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{2}\)
\(S_{xq}=\dfrac{1}{2}SA.AD+\dfrac{1}{2}SA.AB+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=a^2\left(\sqrt{2}+1\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và đáy
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow SA=AD.tan60^0=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3\sqrt{3}}{3}\)
\(SB=SD=\sqrt{SA^2+AD^2}=2a\)
\(S_{xq}=\dfrac{1}{2}SA.AB+\dfrac{1}{2}SA.AD+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=3a^2\)