Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOm}< \widehat{xOy}\left(30^0< 60^0\right)\)
nên tia Om nằm giữa hai tia Ox và Oy
\(\Leftrightarrow\widehat{xOm}+\widehat{yOm}=\widehat{xOy}\)
\(\Leftrightarrow\widehat{yOm}=\widehat{xOy}-\widehat{xOm}=60^0-30^0=30^0\)
Ta có: tia Om nằm giữa hai tia Ox và Oy(cmt)
mà \(\widehat{xOm}=\widehat{yOm}\left(=30^0\right)\)
nên Om là tia phân giác của \(\widehat{xOy}\)(đpcm)
Trong ba tia Om, On, Ok tia Ok nằm giữa hai tia Om, On vì: Trên cùng một nửa mặt phẳng bờ chứa tia Om có mOk^<mOn^( 80°<120°)
(Vẽ hình)
a) Vì hai tia Oy và Ot \(\in\)nửa mặt phẳng bờ Ox; \(\widehat{xOy}\)\(=\)\(80^o\)\(< \)\(\widehat{xOt}\)\(=\)\(120^o\)
\(\Rightarrow\)Tia Oy nằm giữa hai tia Ox và Ot.
\(\Rightarrow\)Ta có: \(\widehat{yOt}\)\(+\)\(\widehat{xOy}\)\(=\)\(\widehat{xOt}\)
\(\Rightarrow\)\(\widehat{yOt}\)\(=\)\(\widehat{xOt}\)\(-\)\(\widehat{xOy}\)
\(=\) \(120^o\)\(-\)\(80^o\)\(=\)\(40^o\)
Vậy \(\widehat{yOt}\)\(=\)\(40^o\)
b) Vì tia Ot là tia phân giác của \(\widehat{yOz}\)
\(\Rightarrow\)\(\widehat{zOt}\)\(=\)\(\widehat{tOy}\)\(=\)\(\frac{1}{2}\)\(\widehat{zOy}\)
Mà ta đã có \(\widehat{tOy}\)\(=\)\(40^o\)
\(\Rightarrow\)\(\widehat{zOy}\)\(=\)\(\widehat{tOy}\)\(:\)\(\frac{1}{2}\)\(=\)\(40^o\)\(:\)\(\frac{1}{2}\)\(=\)\(80^o\)
Vì \(\widehat{xOy}\)\(=\)\(80^o\)\(;\) \(\widehat{zOy}\)\(=\)\(80^o\)
Nên \(\widehat{xOy}\)\(=\)\(\widehat{yOz}\).
c) (Phần này đề cũng sai rồi thì phải. Tại vì ở phần trên chưa có tia On, mà phần này lại là vẽ Om là tia đối của Oy, On)
1. Cho xOy = 135. Trên nửa mặt phẳng bờ Oy chứa Ox, vẽ tia Oz sao cho góc yOz vuông. Gọi Ot là tia đối của tia Oz. Khi đó xOt = 135
2. Cho đường thẳng xy. Trên đường thẳng xy lấy O. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om và On sao cho xOm và mOn là hai góc kề nhau. Biết xOm = 2mOn = 6nOy. Vậy mOn = 54
100 % chính xác!
a) Góc yOm = 1800 - 1000 = 800
Góc yOn = 1800 - 300 = 1500 . => góc yOm < góc yOn => đpcm
b) Góc mOn = góc yOn - góc yOm = 1500 - 800 = 700
c) góc yOt = góc yOm = 800
d) góc aOm = 1/2 góc yOm = 400
góc mOn = 700 => góc aOn = góc aOm + góc mOn = 700 + 400 =1100
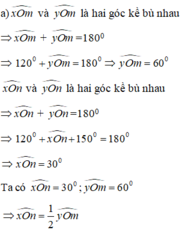
Bạn tự vẽ hình nha
Giải
a,
Trên cùng một nửa mặt phẳng bờ chứa tia Om có góc mOt <mOn(40 <120) nên tia Ot nằm giữa hai tia Om và On
b, Vì tia Ot nằm giữa hai tia Om và On nên:
mOt + tOm= mOn
40 + tOn=120
\(\Rightarrow\)tOn =120-40=80
c, Vì Ox là tia phân giác của nOt nên:
tOx=xOn=\(\frac{nOt}{2}=\frac{80}{2}=40\)
Vì oy là tia phân giác của mOn nên:
mOy=yOn=\(\frac{mOn}{2}=\frac{120}{2}=60\)
Trên cùng một nửa mặt phẳng bờ chứa tia Om có mOy<mOn (60<120) nên tia oy nằm giữa hai tia Om và On
Ta có: mOy +yOn=mOn
60+ yOn=120
yOn= 120 -60 =60