P= cos2x. cot2x + 3cos2x - cot2x +2sin2x có giá trị là:
A.2 B. -2 C.3 D.-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 6 2017
Chọn A.
Ta có: A = cos2x.cot2x + 3cos2x - cot2x + 2sin2x
=( cos2x.cot2x - cot2x) + (2sin2x + 2cos2x) + cos2x
= cot2x( cos2x - 1) + 2 + cos2x
= - cot2x. sin2x + 2 + cos2x
= -cos2x + 2 + cos2x = 2
16 tháng 10 2023
a: \(VT=\dfrac{cot^2x}{1+cot^2x}\cdot\dfrac{1+tan^2x}{tan^2x}\)
\(=\dfrac{cot^2x}{\dfrac{1}{sin^2x}}\cdot\dfrac{\dfrac{1}{cos^2x}}{tan^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{1}{cos^2x}:\dfrac{1}{sin^2x}\)
\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{sin^2x}{cos^2x}\)
\(=cot^2x\)
\(VP=\dfrac{tan^2x+cot^2x}{1+tan^4x}=\dfrac{\dfrac{sin^2x}{cos^2x}+\dfrac{cos^2x}{sin^2x}}{1+\dfrac{sin^4x}{cos^4x}}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}:\dfrac{cos^4x+sin^4x}{cos^4x}\)
\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}\cdot\dfrac{cos^4x}{cos^4x+sin^4x}=\dfrac{cos^2x}{sin^2x}=cot^2x\)
=>VT=VP
b:
\(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}\)
\(=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-cos^2x}{sin^2x}+\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-sin^2x}{cos^2x}\)
\(=\dfrac{sin^2x-cos^4x}{cos^2x\cdot sin^2x}+\dfrac{cos^2x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x+cos^2x-cos^4x-sin^4x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{1-\left(cos^2x+sin^2x\right)^2+2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}\)
\(=\dfrac{2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}=2\)
CM
15 tháng 1 2019
Chọn B
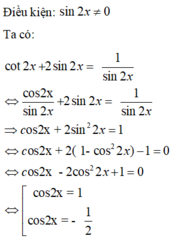
* Với cos 2x = 1 thì sin2x =0 ( không thỏa mãn điều kiện)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2020
a/ \(\left\{{}\begin{matrix}sin\left(1-x\right)\ne0\\cos\left(1-x\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow sin\left(1-x\right).cos\left(1-x\right)\ne0\)
\(\Leftrightarrow sin\left(2-2x\right)\ne0\)
\(\Leftrightarrow2-2x\ne k\pi\Leftrightarrow x\ne1+\frac{k\pi}{2}\)
b và c bạn ghi như vầy ko biết mẫu số nằm ở đâu để tìm điều kiện
TN
1
27 tháng 6 2021
\(a,\tan10.\tan11......\)
\(=\left(\tan10.tan80\right)\left(tan11.tan79\right)....\left(tan44.tan46\right).tan45\)
Mà 10 và 80, 11 và 79, ... là các góc phụ nhau .
\(=tan10.cot10....tan45=1\)
b, Ta có : \(\tan x+\cot x=2\)
\(\Rightarrow\tan^2x+2\tan x\cot x+\cot^2x=4\)
\(\Rightarrow\tan^2x+\cot^2x=4-2=2\)
Ta có : \(\tan^3x+\cot^3x=\left(\tan x+\cot x\right)\left(\tan^2x-\tan x\cot x+\cot^2x\right)=2\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2020
a/
\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos6x-2\left(1-sin^22x\right)=0\)
\(\Leftrightarrow1-\frac{1}{2}\left(cos6x+cos2x\right)-2cos^22x=0\)
\(\Leftrightarrow1-cos4x.cos2x-2cos^22x=0\)
\(\Leftrightarrow2cos^22x-1+cos4x.cos2x=0\)
\(\Leftrightarrow cos4x+cos4x.cos2x=0\)
\(\Leftrightarrow cos4x\left(cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}+k\pi\\2x=\pi+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+\frac{k\pi}{4}\\x=\frac{\pi}{2}+k\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2020
d/
ĐKXĐ: \(sin2x\ne0\) \(\Leftrightarrow2x\ne k\pi\)
\(\Leftrightarrow1+\frac{cos2x}{sin2x}=\frac{1-cos2x}{sin^22x}\)
\(\Leftrightarrow sin^22x+sin2x.cos2x=1-cos2x\)
\(\Leftrightarrow sin^22x-1+sin2x.cos2x+cos2x=0\)
\(\Leftrightarrow-cos^22x+sin2x.cos2x+cos2x=0\)
\(\Leftrightarrow cos2x\left(sin2x-cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin2x-cos2x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin\left(2x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\2x-\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\2x-\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=k\pi\left(l\right)\\x=\frac{3\pi}{4}+k\pi\end{matrix}\right.\)
P = cot2x.(cos2x - 1) +2+cos2x
= \(\left(\frac{cosx}{sinx}\right)^2\)(-sin2x) +2+cos2x
= -cos2x + 2 + cos2x
=2 (Đáp án A)